SYSTEM LICZBOWY STAROŻYTNYCH CHIN

W 1899 r. dokonano znaczącego odkrycia archeologicznego w wiosce Xiao dun  w regionie An-yang w prowincji Henan. Znaleziono tysiące kości oraz żółwich skorup, na których wyryte były znaki starożytnych Chin. Rejon ten był stolicą królów późniejszej dynastii Shang ok. XIV wieku p.n.e. Kości i skorupy były wykorzystywane podczas religijnych ceremonii w trakcie których rozmawiano ze zmarłymi. Pytania ryte były po jednej stronie skorup, a drugą stronę podgrzewano na ogniu – powstałe w ten sposób pęknięcia interpretowane były jako odpowiedzi od zmarłych przodków.
Na tych kościach i skorupach wyryte były również znaki chińskiego systemu liczbowego, dotyczące m.in. liczby poległych wojowników, ilości wziętych niewolników, zabitych zwierząt na polowaniu, liczby dni czy miesięcy, itp. Używano dziesiętnego systemu liczbowego i był to system zarówno addytywny (dodawalny) jak i multiplikatywny (mnożny).
Oto niektóre symbole używane w systemie liczbowym starożytnych Chin:

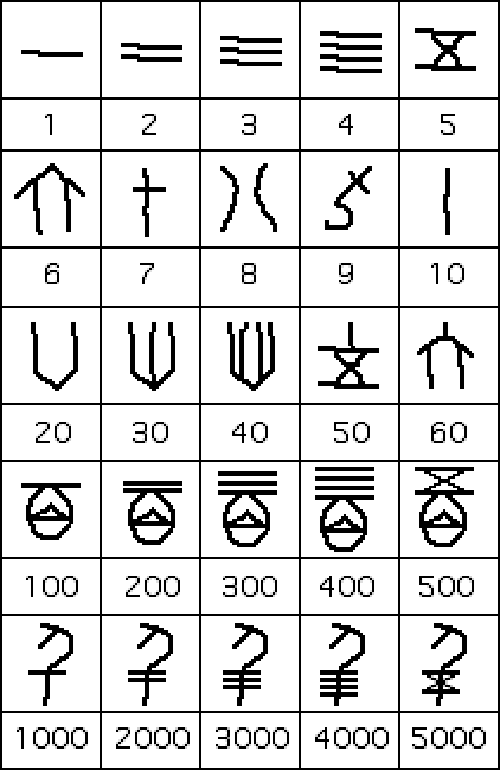Addytywne właściwości przejawiały się tym, że np. 200 reprezentowane jest przez symbol 2, a symbol 300 posiada symbol 3, symbol 400 posiada symbol 4 itd. Podobnie, 2000 posiada nałożony symbol 2,  a symbol 3000 posiada symbol 3. Istnieje symbol dla 10000, nie uwzględniony w tabeli, ale ma postać skorpiona. Największa liczba znaleziona na skorupach to 30000. Dodawalny charakter

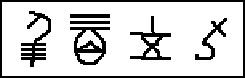
tego systemu liczbowego polega również na tym, że symbole były układane obok siebie, tak więc np. liczbę 4359 reprezentował symbol 4000, za którym znajdował się symbol 300, potem symbol 50 i 9. Oto jak wyglądała liczba 4359:

Nie jest to system pozycyjny, tak wiec niepotrzebne było zero. Na przykład liczba 5080 wygląda następująco:

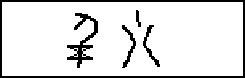A oto  jak wygląda liczba 8873:

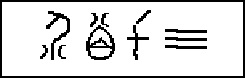Jest kilka ciekawych zagadnień dotyczących systemu liczbowego starożytnych Chin. O ile symbole liczb 1, 2, 3 są zrozumiałe i nie potrzebują wyjaśnień, to pochodzenie symboli pozostałych liczb jest bardziej zawiłe. Istnieją dwie główne teorie wyjaśniające ten problem. Pierwsza teoria sugeruje, iż symbole mają pochodzenie fonetyczne. Na przykład liczba dziewięć wygląda jak haczyk do ryb, i możliwe, że dźwięk słowa 9 był podobny do słowa „haczyk na ryby”. Symbol 1000 jest podobny do człowieka, i podobnie, możliwe było, że słowo 1000 w starożytnych Chinach było podobne fonetycznie do słowa „człowiek”. Druga teoria o symbolach mówi, że liczby i prawie wszystkie litery w późnym okresie Shang, były używane tylko jako część ceremonii religijnych. Czyli symbole te maja znaczenie religijne. Możliwe również, że niektóre liczby podlegają pierwszej teorii a inne teorii drugiej. Symbole takie jak skorpion oznaczają bardzo dużą liczbę (10000), gdyż prawdopodobnie widok gniazda skorpionów wydawał się bardzo dużą ilością dla ludzi tamtych czasów. Prawdopodobnie symbol 100 reprezentuje palec u nogi, gdyż ludzie liczyli do 10 na swoich palcach u rąk, a następnie do 100 wykorzystując palce u nóg, a 1000 reprezentuje człowieka, który policzył wszystkie części ciała. Od IV wieku p.n.e. zaczęto używać innej formy liczb, gdy to rozpowszechniły się tabliczki do liczenia. Tabliczka składała się z szachownicy z rzędami i kolumnami. Liczby były reprezentowane przez małe pręty wykonane z bambusa lub kości słoniowej. Liczba była tworzona w rzędzie razem z jednostkami położonymi w kolumnie położonej po skrajnej prawej stronie, następnie, dziesiątki tworzone były w następnej kolumnie  na lewo, setki w następnej lewej kolumnie, itd. Najbardziej znaczącą cechą tego systemu było to, że był to naturalny system pozycyjny wartości liczbowych. Skrajna prawa kolumna reprezentowała jedność, następna kolumna 10, itd. Liczby 1 do 9 musiały być tworzone z przesuwających się prętów. Wymyślono następujące dwie metody notacji cyfr:

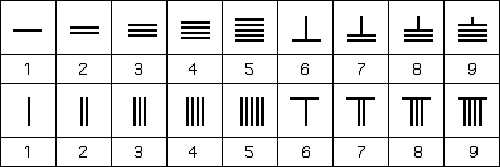Notacja ta mogła jednak prowadzić do pewnych pomyłek.  Na przykład co oznaczało ||| ? Mogło oznaczać 3, lub 21, lub 12 lub nawet 111. Pręty przesuwające się lekko wzdłuż rzędów, lub nie usytuowane centralnie w swoich kwadratach, prowadziły do reprezentowania nieprawidłowych liczb. Jednak Chińczycy wymyślili sposób aby temu zapobiec. Używali obydwie wyżej przedstawione formy liczb. W kolumnie jednostek używali formę z niższego rzędu,

a w kolumnie dziesiątek używali formę z wyżej położonego rzędu, postępując dalej alternatywnie. Na przykład 1234 reprezentowane jest na  liczydle przez:

 
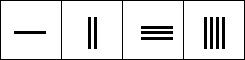 a 45698 następująco:

Nadal nie potrzebne było zero, gdyż w miejscu zera zostawiano puste miejsce na liczydle. Alternatywne ustawianie liczb (posługując się na zmianę wyższym i

 niższym rzędem) pomagało w pokazywaniu takiego pustego miejsca. Na przykład 60390 reprezentowane było jako:

Starożytne arytmetyczne teksty opisywały jak wykonywać operacje matematyczne na liczydle.
W pierwszym rozdziale Sunzi suanjing (Podręcznik Matematyki), autora Sun Zi, opisuje jak posługiwać się prętami obliczeniowymi do mnożenia, dzielenia i obliczania pierwiastków z liczb.
Xiahou Yang napisał w V wieku podręcznik matematyki Xiahou Yang suanjing, w którym podaje, że aby pomnożyć liczbę przez 10, 100, 1000 lub 10000 należy tylko przesunąć w lewo pręty w liczydle o 1, 2, 3 lub 4 kwadraty. I podobnie, aby podzielić przez 10, 100, 1000 lub 10000 pręty należy przesunąć w prawo o 1, 2, 3 lub 4 kwadraty. Jest zdumiewające to, iż Ziahou Yang prawdopodobnie rozumiał dodatnie potęgi liczby 10, oraz ułamki dziesiętne jako ujemne potęgi liczby 10. Ilustruje to duże znaczenie liczb używanych w tabliczkach liczbowych. Liczby te były również używane w pisanych tekstach matematycznych
W XIV wieku w Chinach zaczęto używać liczydła. Tabliczki obliczeniowe oraz liczydła były wynalazkiem chińskim. Liczydła zamiast pretów, posiadały paciorki przesuwające się wzdłuż drutów.
Arytmetyczne zasady liczenia na liczydłach były takie same jak na tabliczkach obliczeniowych. Nawet pierwiastki kwadratowe i sześcienne można było obliczać, ale niestety, liczydła przeważnie używali kupcy, którzy tylko wykonywali operacje dodawania i odejmowania.

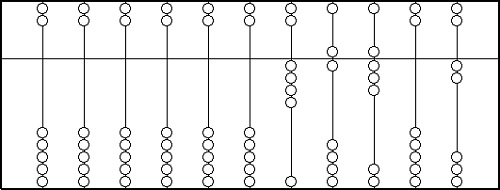Ilustracja liczydła z liczbą 46802.

Dla liczb do 4 przesunąć należy wymaganą liczbę paciorków z dolnej części do środkowego pręta. Na przykład na skrajnym prawym drucie prezentowane jest 2. W przypadku liczby 5 należy przesunąć jeden paciorek położony powyżej środkowego pręta w dół (reprezentujący 5), oraz 1, 2, 3 lub 4 paciorki z dołu w górę do środkowego pręta dla liczb 6, 7, 8 lub 9, odpowiednio. Na przykład na drucie trzecim od prawej strony prezentowana jest liczba 8 (5 na górnym paciorku i trzy paciorki poniżej).
Można zadać pytanie dlaczego każdy pręt posiada ilość paciorków wystarczająca do prezentacji liczby 15? Aby ułatwić pośrednie obliczenia – liczby większe od 9 mogły być przechowywane na pojedynczym pręcie podczas wykonywania kalkulacji (rodzaj pamięci); jednak przy finalizowaniu obliczeń zawartość pamięci musiała być przeniesiona  na pręt położony na lewo.

Artykuł powstał na podstawie tekstu napisanego przez JJ O'Connor i E F Robertson

Zapraszamy do artykułu, w którym poznamy historję notacji liczb stosowaną obecnie w Euroie