|
|
 |
|
Cyfrowa historia
Bez cyfr trudno wyobrazić sobie matematykę. Wielu zapewne matematyka kojarzy się wyłącznie z cyframi, w przeciwieństwie do dyscyplin humanistycznych, operujących przede wszystkim słowem. Życie codzienne w dużym stopniu również zdominowane jest przez cyfry – gdy patrzymy na zegarek, płacimy za zakupy, zapisujemy datę itd. Cyfry stały się czymś tak powszechnym i oczywistym, że mogłoby się wydawać, iż takie są od zawsze, niezmienne. Nic bardzej mylnego. Ich zapis zmieniał się na przestrzeni wieków, a dodatkowo w różnych kulturach obowiązywały różne systemy cyfrowe. Cyfry używane współcześnie zaczęły zdobywać przewagę dopiero w epoce nowożytnej.
|
|
Cyfry arabskie
Cyfra to umowny, symboliczny znak pisarski służący do zapisywania liczb. Słowo cyfra pochodzi z języka arabskiego od słowa sifr, co oznacza zero. Obecnie używane cyfry arabskie tak naprawdę są pochodzenia hinduskiego i zostały zapożyczone przez Arabów z Indii. Najstarsze dokumenty zawierające znaki liczb, czyli cyfry, pochodzą z czwartego tysiąclecia p.n.e. Ciekawostką jest bardzo późne pojawienie się znaku zero, około V wieku n.e. Tłumaczyć to można trudnością uznania zera za liczbę. Pojęcie liczby znacznie łatwiej jest bowiem powiązać z pewną grupą przedmiotów, gdy mowa np. o pięciu książkach czy dwunastu komputerach. Trudniej jest natomiast uznać, że zero, czyli „nic”, ma podobny status do innych liczb. Innymi słowy – liczby stwierdzają istnienie jakichś przedmiotów, podczas gdy zero stwierdza ich brak. Zapis cyfr indyjsko-arabskich w ujęciu historycznym przedstawia tabelka poniżej.
|
|
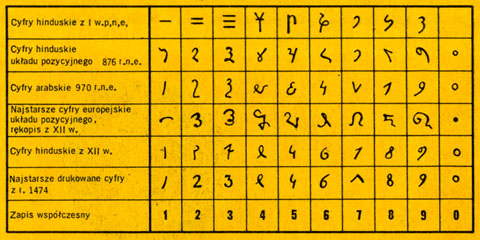 |
W Europie indyjsko-arabski system zapisywania cyfr pojawił się wraz z podbojami arabskimi w VIII wieku n.e. Najstarszy na naszym kontynencie zapis liczby w systemie przejętym od Arabów pochodzi z 1138 roku i znajduje się na monetach wybitych przez Rogera z Sycylii. Wielkie zasługi w rozpowszechnieniu w Europie indyjsko-arabskiego zapisu cyfr miał włoski matematyk Leonardo Fibonacci (1175-1250), który swoją wiedzę zdobywał w środowisku uczonych arabskich, podczas swoich podróży po Europie i krajach Wschodu. W 1202 roku wydał on książkę Liber Abaci (co można przetłumaczyć jako Księga rachunków albo Księga abaka; abak to dawny przyrząd używany do przeprowadzania rachunków), w której rozpropagował nowe zasady numeracji. Fibonacci bardzo entuzjastycznie pisał: „Jest dziewięć znaków hinduskich, oto one: 9, 8, 7, 6, 5, 4, 3, 2, 1. Za pomocą tych znaków i znaku 0, który po arabsku zwie się sifr, można napisać wszelką, jaką kto chce, liczbę”. W swojej książce umieścił również tablicę, w której pewne liczby zapisane były dla porównania jednocześnie rzymskimi i indyjsko-arabskimi cyframi. Proponowany przez Fibonacciego zapis cyfr nie od razu zyskał uznanie. Jeszcze w 1229 roku rada miejska Florencji zabroniła używania arabskich cyfr i nakazała posługiwanie się symbolami rzymskimi lub wpisywanie liczb słownie. Wiązało się to z częstymi fałszerstwami – zero można było łatwo przerobić na 6 lub 9, a poza tym bardzo trudno docierała do ówczesnej świadomości możliwość istnienia cyfry 0, która znaczy „nic”. Polska była jednym z pierwszych krajów, który wprowadził u siebie cyfry indyjsko-arabskie. Najstarszy polski tekst matematyczny, w którym występuje taki właśnie zapis cyfr, pochodzi z 1397 roku, pierwsze monety z nowymi cyframi pojawiły się natomiast w naszym kraju w 1507 roku.
|
|
System liczbowy indyjsko-arabski nazywany jest układem dziesiątkowym pozycyjnym.
Dziesiątkowy – to znaczy taki, że każda następna jednostka wyższego rzędu zawiera 10 jednostek rzędu bezpośrednio niższego – setka zawiera 10 dziesiątków, tysiąc zawiera 10 setek itd.
Pozycyjny – dlatego że znaczenie cyfry jest zależne od miejsca (pozycji), które zajmuje ona w liczbie – np. liczba 1115 zawiera trzy jednakowe cyfry, każda jednak ma zupełnie inne znaczenie: 1 umieszczona na drugim miejscu, licząc od prawej strony, oznacza liczbę 10, 1 znajdująca się na trzecim miejscu od prawej strony oznacza liczbę 100, a cyfra 1 na początku liczby oznacza liczbę 1000.
|
|
 |
 |
Leonardo Fibonacci w swojej książce Liber Abaci oprócz tego, że spopularyzował cyfry arabskie, to przedstawił w niej wiele ciekawych problemów-zadań matematycznych. Oto trzy z nich:
1. Dwa ptaki wylatują w tym samym momencie ze szczytów dwóch wież, odległych o 50 metrów. Wysokość jednej wieży to 30 metrów, a drugiej – 40 metrów. Lecąc z tą samą prędkością, dolatują w tym samym momencie do fontanny znajdującej się pomiędzy dwiema wieżami (na poziomie gruntu, poziom 0). W jakiej odległości od podstawy każdej wieży znajduje się fontanna.
2. Trzech mężczyzn znalazło sakiewkę zawierającą 23 denary. Pierwszy powiedział do drugiego: „Jeżeli dodam te pieniądze do swoich, to będę miał dwa razy więcej od ciebie”. |
|
Drugi podobnie zwrócił się do trzeciego: „Ja zaś, jeżeli wezmę te pieniądze, będę miał trzy razy więcej od ciebie”. W końcu trzeci powiedział do pierwszego: „Ja, dodając te pieniądze do swoich, będę miał cztery razy więcej niż ty”. Ile denarów miał każdy z nich.
3. Kupiec podczas swojej podróży handlowej do Wenecji podwoił tam swój początkowy kapitał, a następnie wydał 12 denarów. Potem udał się do Florencji, gdzie znowu podwoił liczbę posiadanych denarów i wydał 12. Po powrocie do Pizy po raz kolejny podwoił swój majątek, wydał 12 denarów i... został bez grosza. Ile denarów miał na początku?
|
|
Cyfry rzymskie
Cyfry rzymskie znane są już od ponad MM lat. Jakkolwiek od momentu pojawienia się cyfr arabskich zakres ich używania znacznie się zmniejszył, to jednak stosuje się je również obecnie. Można je jeszcze zobaczyć na tarczach zegarowych, za ich pomocą oznacza się miesiące w datach (np. 21 IX – 21 września), a także wieki jako okresy w dziejach ludzkości (np. VII wiek, XX wiek itp.), numeruje się nimi rozdziały książek lub artykułów (np. I rozdział, IV rozdział itd.). Rzymski zapis cyfrowy został przejęty i zmodyfikowany przez Rzymian od Etrusków ok. D lat p.n.e. Etruskowie to lud zamieszkujący w starożytności północną Italię (Eturię). Cywilizacja etruska największy rozkwit przeżywała w latach ok. DC – XXXD p.n.e., później została wchłonięta przez Rzymian.
W systemie rzymskim do zapisu liczb używanych jest siedem znaków cyfrowych (liter):
Znak I V X L C D M
Wartość 1 5 10 50 100 500 1000
Geneza poszczególnych rzymskich znaków cyfrowych jest następująca:
I (1) – pochodzi od pionowej kreski, oznaczającej jeden element.
V (5) – jest górną połową znaku X (10).
L (50) – jest najprawdopodobniej dolną połową znaku C (100), chociaż nie ma w tej sprawie jednomyślności.
C (100) – od łacińskiego słowa centum – sto.
M (1000) – od łacińskiego słowa mille – tysiąc.
D (500) i X (10) – ich pochodzenie nie zostało dowiedzione, być może pochodzą od nieznanych jeszcze etruskich znaków.
Rzymski system liczbowy jest systemem addytywnym (od łacińskiego słowa additivus – dodający). Cyfrowy zapis liczb polega na dodawaniu lub odejmowaniu znaków o określonym nominale. Cyfry jednakowe są zawsze dodawane (np. II = I + I = 1 + 1 = 2; CC = C + C = 100 + 100 = 200), cyfry mniejsze stojące za większymi są również dodawane (np. DXI = D + X + I = 500 + 10 + 1 = 511; LVII = L + V + I + I = 50 + 5 + 1 + 1 = 57), cyfry mniejsze stojące przed większymi są odejmowane od tych większych (np. IX = X – I = 10 – 1 = 9; CM = M – C = 1000 – 100 = 900). A oto inne przykłady tworzenia cyfr rzymskich: IV – 4, VI – 6, XXX – 30, XC – 90, MXXXVII – 1037, MCMLIX – 1959, MMVII – 2007. Liczba, nad której zapisem cyfrowym umieszczona była pozioma kreska, zwiększała swoją wartość tysiąckrotnie, na przykład:
___ __ ______
XII = 12 000; CL = 150 000; DCLXXV = 675 000 itd.
|
|
Cyfry greckie
W starożytnej Grecji ukształtowały się dwa odmienne zapisy cyfrowe i wynikało to z różnic między Grecją właściwą a koloniami. Ateński sposób przedstawiania liczb za pomocą cyfr, pochodzący z ΓI wieku p.n.e. i używany do I wieku p.n.e., polegał na zapisywaniu początkowych liter nazw liczb (czyli początkowych liter słów oznaczających liczby) zamiast tych liczb. Wjątkiem był zapis liczby 1, który przybierał postać pionowej kreski, i zapis liczb 2, 3, 4 przedstawiany jako wielokrotność zapisu liczby 1. I tak:
I, II, III, IIII – oznaczało 1, 2, 3, 4.
Γ – oznaczało 5, ponieważ gente po ateńsku znaczy 5.
Δ – oznaczała 10, ponieważ deka po grecku znaczy 10.
Η – oznaczało 100, ponieważ hekaton znaczy 100.
Χ – oznaczało 1000, ponieważ chilioi znaczy 1000.
Μ – oznaczało 10 000, ponieważ myrias znaczy 10 000.
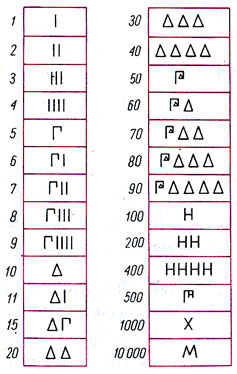
A oto tabelaryczne zestawienie cyfr greckich w systemie ateńskim:
|
|
 |
 |
Aby zapisać jakąś liczbę, umieszczano kolejno od lewej do prawej strony odpowiednie cyfry od największej do najmniejszej, żądana liczba była sumą poszczególnych liczb wyrażanych przez następujące po sobie cyfry. Na przykład:
ΓIII = 8; ΔΔΓI = 26;
ΗΔΔΔΔΓ = 145; ΧΗΗΔΓIII = 1218;
ΜΧΧΧΗΗΗΗΔIIII = 13 414.
Można również dla lepszego zrozumienia greckiego zapisu cyfr spróbować zobaczyć, jak zapis na podobnych zasadach przedstawiałby się w języku polskim. I niech więc oznacza 1; P (od pierwszej litery słowa pięć) niech oznacza 5; D (od pierwszej litery słowa dziesięć) niech oznacza 10; S (od pierwszej litery słowa sto) niech oznacza 100; T (od pierwszej litery słowa tysiąc) niech oznacza 1000. Na podstawie takiego hipotetycznego zapisu cyfr można już zapisywać liczby w podobny sposób, jak to czynili Grecy. Na przykład PII = 7; DDP = 25;
SDDDPI = 136; TTTSSDDPIII = 3228 itp. |
|
Inaczej przedstawiał się joński system cyfrowy, pochodzący z kolonii greckich w Azji Mniejszej (Milet) i Aleksandrii. Najstarszy zapis tych znaków pochodzi z Γ wieku p.n.e. Polegał on na wykorzystaniu kolejnych liter alfabetu jako cyfr, na przyporządkowaniu każdej literze alfabetu greckiego jednej cyfry. Żeby system był kompletny, do liter greckich dodano także (dla oznaczenia 6, 90 i 900) trzy litery z alfabetu semickiego. Wzajemne powiązanie liter i cyfr przedstawia tabela:
|
|
Liczby tworzone były przez zestawienie obok siebie znaków cyfrowych w porządku od lewej strony do prawej. Nad całym wyrażeniem umieszczano poziomą kreskę dla odróżnienia go od liter, np.:
__ __ ___
κβ = 22; πθ = 89; ωλδ = 834.
Dla oznaczenia tysięcy przed odpowiednią literą umieszczano przecinek, na przykład: ,α = 1000;
,β = 2000; ,γ = 3000 itd. I w ten sposób zapisywano większe liczby:
____
,βφκε = 2525;
____
,δχογ = 4673;
____
,ητπζ = 8387 itp.
Największe liczby tworzone były za pomocą litery M, która oznaczała
10 000. Zapis wyglądał w ten sposób, że nad literą M umieszczano liczbę dziesiątków tysięcy tej liczby. Tak np.:
ζ
M = 7 razy po 10 000 = 70 000;
πα
M = 81 razy po 10 000 = 810 000;
φλδ
M,βωογ = 5 342 873.
Powyższy joński zapis cyfrowy był najbardziej powszechny i w II wieku p.n.e. wszedł do urzędowego użycia. Z czasem jednak w ciągu setek lat ulegał on pewnym modyfikacjom, szczególnie dotyczyło to zapisywania największych liczb.
(dt) |
 |
 |
|
|
 |
|

