|
|
 |
NAJSTARSZA ZAGADKA ŚWIATA - STOMACHION |
|
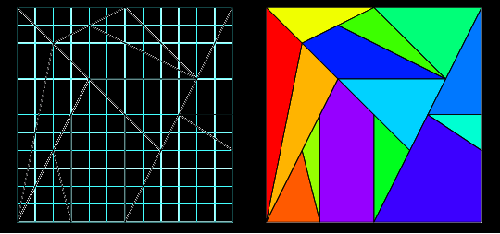 |
Stomachion, zwany też loculus Archimedius (po łacinie: pudełko Archimedesa) – starogrecka łamigłówka i gra składająca się z 14 elementów, z których należy złożyć kwadrat lub inny, z góry założony kształt. Przypomina bardzo chiński tangram, który jest złożony jednak z tylko 7 elementów. Człowiekiem, który jako pierwszy obliczył, na ile sposobów można to zrobić, był wg legend Archimedes (287 BC - 212 p.n.e.). Tekst Archimedesa został odnaleziony na palimpseście pod modlitwami i był odczytywany na początku XXI wieku oraz poddany konserwacji. Legenda mówi, że zwoje Archimedesa, zwane Palimpsest, zostały pocięte i ponownie nadpisane. Palimpsest – rękopis spisany na używanym już wcześniej materiale piśmiennym, z którego usunięto poprzedni tekst, najczęściej w celu zmniejszenia kosztów owego materiału. W październiku 1998 r. w Nowym Jorku za 2 miliony dolarów sprzedano manuskrypty niektórych prac Archimedesa, znanych jako Palimpsesty Archimedesa. Kwadrat stomachiona ma długość boku równą 12, części mają powierzchnie: 3, 3, 6, 6, 6, 6, 9, 12, 12, 12, 12, 12, 21, oraz 24, co daje im powierzchnie względne: 1, 1, 2, 2, 2, 2, 3, 4, 4, 4, 4, 4, 7, oraz 8. Zauważmy, że każda wartość jest liczbą całkowitą! |
|
 |
 |
Podobnie jak w chińskim tangramie, zadanie polega na ułożenie z części interesującego kształtu, jak np. wyżej pokazanego słonia.
|
|
W listopadzie 2003 r., Bill Cutler odkrył, przy wykorzystaniu komputera, iż istnieje 536 możliwych różnych ułożeń części, które tworzą kwadrat, co pokazano powyżej, gdzie rozwiązania równoważne utworzone poprzez obrót lub odbicie lustrzane są uważane jako identyczne |
|
Najczęściej prezentowany jest układ pokazany obok: |
 |
 |
|
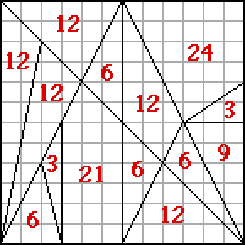
Zbadajmy ten schemat poprzez zmierzenie pola każdego wieloboku: |
|
 |
 |
Całkowita powierzchnia wynosi 144 jednostek. Każda część jest proporcjonalna do powierzchni kwadratu. Na przykład, pole „21” stanowi 7/48 powierzchni kwadratu. Zauważmy, że każda wartość jest liczbą całkowitą! |
|
Upraszczając przez wspólny podzielnik 3, otrzymujemy następujący schemat: |
|
Widzimy, że powierzchnia każdej części układanki Archimedesa stanowi wielokrotność 1/48 powierzchni całego kwadratu. Rozdzielenie części oraz ich odpowiednie przegrupowanie pozwala zbudować proste ułamkowe pola |
|
Wiele innych form można uzyskać przy pomocy części Stomachiona, na przykład następujące są najpopularniejsze: |
|
Kolejne wieloboki mogą być zbudowane przy wykorzystaniu wszystkich lub niektórych części problemu Archimedesa, np.: następujące dziesięcioboki w kształcie diamentu: |
|
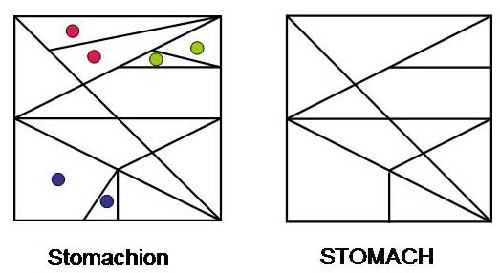
Oryginalny Stomachion składa się z 14 części tworzących kwadrat, tak jak to pokazano na rysunku. Jednakże, można wykazać, iż dwie części z czerwonymi kropkami muszą sąsiadować ze sobą w dowolnym ułożonym kwadracie. Tak samo z częściami z dwoma zielonymi oraz dwoma niebieskimi kropkami. Możemy dlatego ułożyć i rozważać kwadrat z 11 części, zwany stomachem. |
|
 |
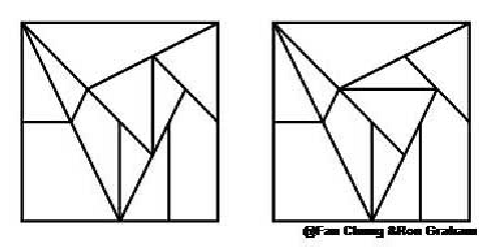
Pytanie 1: Ile różnych rozwiązań istnieje dla stomacha? Czyli, ile istnieje sposobów ułożenia części w kwadrat, wykorzystując „zmodyfikowane” części? Odpowiedź zależy od tego co rozumiemy przez „różne”. Jeżeli nie bierzemy pod uwagę części przystające, wtedy odpowiedź brzmi: 2144 (= 8 x 268). Jeżeli weźmiemy pod uwagę dwie części różniące się tylko poprzez obrót oraz/lub odbicie lustrzane, wtedy odpowiedź brzmi: 268. Jednak gdy uwzględnimy obie te możliwości, to otrzymujemy całkowitą sumę równą:17152. Pytanie 2: Czy można zbudować inną dowolną konfigurację z innej dowolnej konfiguracji dzięki „prostym” przesunięciom? Przez “proste” przesunięcie, rozumiemy odbicie symetryczne lub rotacja symetrycznego podregionu utworzonego przez zestaw sąsiadujących ze sobą części stomacha. Aby rozwiązać problem, tworzymy graf ze zbiorem wierzchołków składający się z 268 węzłów, każdy odpowiadający unikalnemu rozwiązaniu. Dwa wierzchołki są przyległe/sąsiednie względem siebie, jeżeli istnieje “proste” przesunięcie przekształcające jedno w drugie. Pytanie 2 może też brzmieć: „Czy graf stomacha jest połączony?”. Odpowiedź na Pytanie 2 brzmi „prawie”, ale nie całkiem „tak”. Graf stomacha ma olbrzymi połączony ze sobą komponent składający się z 266 wierzchołków, oraz mniejszy komponent składający się z 2 wierzchołków, co pokazano poniżej; |
|
 |
Pytanie 3: Czy istnieje efektywne przechodzenie przez wszystkie części w Stomacha? Mamy tu cykl Hamiltona, tj. cykl zawierający każdy wierzchołek dokładnie raz wraz z powrotem do początkowego punktu startowego - w naszym dużym komponencie składający się z 266 wierzchołków. Cykl Hamiltona to taki cykl w grafie, w którym każdy wierzchołek grafu przechodzony jest tylko jeden raz (oprócz pierwszego wierzchołka) . Znalezienie cyklu Hamiltona o minimalnej sumie wag krawędzi jest równoważne rozwiązaniu problemu komiwojażera. Grafy zawierające cykl Hamiltona nazywamy hamiltonowskimi. |
|
|
 |
|

