Związek notacji liczb z kalendarzem u Mayów

Hernán Cortés 18 lutego 1519 r. popłynął z Hiszpanii w kierunku półwyspu Yucatán. Jego armada liczyła 11 okrętów, 508 żołnierzy, 100 żeglarzy i 16 koni. Wylądował w pobliżu Tabasco na północnym wybrzeżu półwyspu Yucatán. Napotkał niewielki opór miejscowej ludności, która później wręczyła mu liczne prezenty włącznie z 20 kobietami. Ożenił się z jedną z nich imieniem Malinche. Kobieta ta później odegrała rolę tłumacza dla Cortés’a w czasie jego podbojów.
Ludność półwyspu Yucatán była potomkami starożytnej cywilizacji Mayów, która zaczęła chylić się ku upadkowi od ok. roku 900 n.e. Następnie Cortés’a podbił cywilizację  Azteków, znajdującą się na terenie dzisiejszego Meksyku. Zdobył miasto Tenochtitlán w 1519 r.(miasto to zostało odbudowane pod nazwą Meksyk w 1521 r.). Imperium Azteków poddało się Cortés’owi ostatecznie w 1521 r.
Aby zrozumieć jak wiedza Mayów dotarła do nas, musimy poznać jeszcze jednego Hiszpana – Diego de Landa, który wstąpił do zakonu franciszkanów w 1541 r. w wieku 17 lat. Domagał się, aby go wysłano do Nowego Świata jako misjonarz. Landa pomagał Mayom na Yucatanie i starał się jak mógł, aby ochronić ich przed nowymi hiszpańskimi władcami.
Jednakże pomimo życzliwości dla Mayów, czuł odrazę dla ich religijnych praktyk. Dla oddanego chrześcijanina jakim był Landa, religia Mayów ze swoimi piktogramami i wizerunkami oraz tekstami hieroglifami wydawała się dziełem diabła. Nakazał zniszczenie wszystkich bożków Mayów oraz spalenie wszystkich ich ksiąg. Landa był zdziwiony tym, jak bardzo zmartwiło to Mayów. Żałował później swoich czynów i próbował ich usprawiedliwić w książce „Relación de las cos as de  Yucatán” (1566r.). Opisał hieroglify, obyczaje, świątynie, praktyki religijne oraz historię Mayów. Książkę tę dopiero odnaleziono w 1869r.
Jednak niewielka liczba dokumentów przetrwała zniszczenia Landy. Najważniejszymi ocalałymi dziełami są: Kodeks Drezdeński, znajdujący się w Sächsische Landesbibliothek w Dreźnie, Kodeks Madrycki obecnie w Muzeum Ameryki w Madrycie oraz Kodeks Paryski w Bibliothéque Nationale w Paryżu.
Kodeks Drezdeński stanowi traktat o astronomii, który został skopiowany w XI wieku n.e. z oryginalnego dokumentu (VII w. n.e.).

Nas interesuje Okres Klasyczny Mayów, czyli od 250 do 900 r. n.e., z tym, że cywilizacja ta początek swój bierze od ok. 2000 r.  p.n.e. Mayowie Okresu Klasycznego zbudowali duże miasta – ok. 15 ich odkryto na półwyspie Yucatán. Miasto Tikal liczyło aż 50 tysięcy mieszkańców, 3000 samodzielnych budynków, włącznie z pałacami, świątyniami, grobami świętych, domami, tarasami, groblami, placami i olbrzymimi zbiornikami do przechowywania wody deszczowej. Władcami byli kapłani astronomowie, którzy kontrolowali ludność dzięki swoim religijnym rytuałom. Rolnictwo wraz z rozbudowanymi systemami irygacyjnymi stało na wysokim poziomie.
Ważną rolę w społeczeństwie odgrywała astronomia i kalendarze, które wymagały znajomości matematyki. I rzeczywiście Mayowie opracowali bardzo wyrafinowany system liczbowy. Na owe czasy był to najbardziej zaawansowany system na całym świecie.
Pozycyjny system liczbowy Mayów oparty był na systemie dwudziestkowym. Powstał najpewniej dlatego, że Mayowie posługiwali się przy liczeniu palcami rąk oraz nóg.

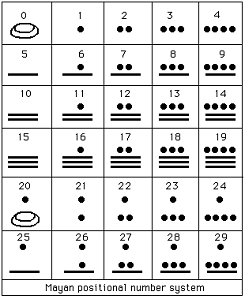
 Pomimo, że był to system dwudziestkowy to widać jednak jak ważną rolę odgrywała liczba pięć. Warto zauważyć, że system ten ma tylko trzy symbole liczbowe (prawdopodobnie w czasie liczenia symbol jedności stanowił kamyk, symbol liniowy był patykiem, a zero muszlą). Pozycyjny system liczbowy Mayów był systemem dwudziestkowym. Nasz system dziesiętny dzieli się
na pozycje: 1, 10, 100, 1000, 10000 etc., a system
Mayów na pozycje: 1, 20, 400, 8000, 16000 etc.
W systemie dziesiętnym istnieje dziesięć możliwych cyfr dla każdej pozycji liczbowej [0 – 9]; w systemie Mayów istnieje 20 możliwych cyfr dla każdej pozycji
liczbowej [0-19]. Np. w systemie dziesiętnym
31 = 10x3 + 1, natomiast u Mayów 31 = 20 +11. Mayowie odkryli i używali zero.

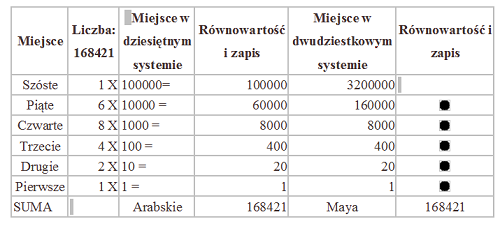
Pozycje liczbowe w dwudziestkowym pozycyjnym systemie Mayów rosną odpowiednio pomnożone przez 20. Dla porównania liczba 168 421 w obu systemach liczbowych:

Liczby w systemie Mayów mogą być pisane pionowo lub poziomo.  W zapisie pionowym, linie są położone poziomo a kropki są stawiane nad nimi. W tym przypadku dwudziestkowe pozycje rosną od bazy w górę.
W zapisie  poziomym linie są położone pionowo a kropki stawiane są na lewo; tutaj dwudziestkowe pozycje rosną na lewo od pierwszego zapisu.
Jednakże system niniejszy nie był pozycyjnym systemem liczbowym w ścisłym słowa tego znaczeniu.
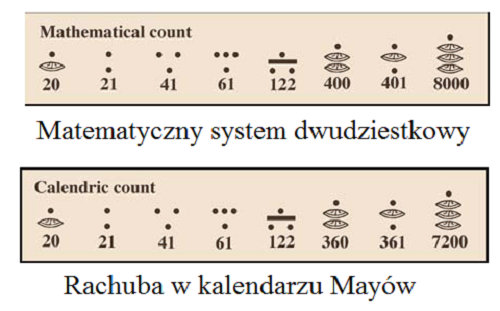
W dwudziestkowym systemie pierwsza cyfra wskazywałaby ilość jednostek do 19, następna wskazywałaby ilość dwudziestek aż do 19, następna ilość 400 aż do 19, itd.
System Mayów rozpoczyna się w ten sposób z jednostkami do 19 oraz dwudziestkami  do 19, jednak zmiana następuje na trzecim miejscu i tu wskazywana jest liczba 360 do 19, zamiast 400. Potem system powraca do normalnych wielokrotności dwudziestek, tak więc na czwartym miejscu jest liczba 18 x 20^2, następna liczba to 19 x 20^3, itd. Na przykład [8; 14; 3; 1; 12] odpowiada:
12 + 1 x 20 + 3 x 18 x 20 + 14 x 18 x 20^2 + 8 x 18 x 20^3 = 1253912.
Jako drugi przykład [9; 8; 9; 13; 0] odpowiada:
0 + 13 x 20 + 9 x 18 x 20 + 8 x 18 x 20^2 + x 18 x 20^3 = 1357100.
Oba powyższe przykłady znaleziono w ruinach miast Mayów i ich znaczenie jest opisane w dalszej części.

Wyżej opisany system występuje w Kodeksie Drezdeńskim i jest to jedyny system, na który istnieją dowody pisemne. Prawdopodobnie używali go kapłani oraz astronomowie do kalkulacji astronomicznych i kalendarzowych.
Mayowie używali dwóch rodzaj kalendarzy. Pierwszy był kalendarzem rytualnym zwany Tzolkin, składający się z 260 dni. Zawierał 13 „miesięcy”, a każdy składał się z 20 dni. Miesiące były nazwane imionami 13 bogów, a 20 dni były ponumerowane od 0 do 19. Oto glify i nazwy tych 20 dni:

Drugi był państwowym kalendarzem składającym się z 365 dni, zwany Haab. Zawierał 18 długich miesięcy z nazwami wydarzeń religijnych i rolniczych oraz jeszcze jednego krótkiego „miesiąca” z 5 dniami zwany Wayeb. Każdy długi miesiąc składał się z 20 dni (też ponumerowane od 0 do 19). Wayeb był uważany za nieszczęśliwy okres. W tym czasie Mayowie nie myli się, nie czesali i nie wykonywali żadnej ciężkiej pracy w okresie tych 5 dni. Urodzeni w tym okresie mieli mieć pecha w życiu i pozostawać biedni i nieszczęśliwi przez całe życie. Dlaczego kalendarz rytualny został oparty na okresie 260 dni? Nie ma satysfakcjonującej odpowiedzi na to pytanie. Jedni sugerują, iż Mayowie żyli  w strefie tropikalnej i słońce znajdowało się na niebie bezpośrednio nad nimi dwa razy  w roku. Może mierzyli 260 dni oraz 105 dni jako kolejne okresy pomiędzy najwyższymi położeniami słońca na niebie (jest to prawda dla półwyspu Yucatán). Inna teoria mówi, iż Mayowie mieli 13 bogów ze „świata wyższego”, a liczba 20 była liczbą symbolizującą człowieka, tak więc dzięki przydzieleniu każdemu bogowi 20 dniowego miesiąca otrzymujemy kalendarz rytualny z 260 dniami. Mając dwa kalendarze, jeden z 260 dniami i drugi z 365 dniami, można obliczyć, iż oba powrócą do tego samego cyklu po (260 x 365) = 18980 dniach. Nastąpi to po 52 państwowych latach lub 73 rytualnych latach i rzeczywiście Mayowie mieli święty cykl składający się z 52 lat. Drugą ważną rolę w kalendarzu odgrywała planeta Wenus. Astronomowie Mayowie obliczyli jego okres synodyczny (po którym to okresie wraca ona do tego samego położenia na niebie) równy 584 dni. Po tylko dwóch cyklach 52-letnich Wenus wykona 65 obrotów i będzie też znajdowała się w tym samym położeniu. Ta niezwykła zbieżność była powodem do wielkich uroczystości urządzanych co 104 lata. Istniała również trzecia metoda mierzenia czasu przez Mayów, nie będąca jednakże kalendarzem w ścisłym słowa tego znaczeniu. Była to skala czasowa oparta na mniemanej dacie stworzenia świata i czas był mierzony od tego momentu. Data ta to 12 sierpnia 3113 rok p.n.e.. Należy wspomnieć, że nie wszyscy uczeni zgadzają się, iż ta data rozpoczęła tzw. „Długie Odliczanie”. Można byłoby spodziewać się, iż ta metoda mierzenia czasu powinna odmierzyć nam liczbę lat kalendarzy rytualnych lub państwowych. Niestety nie zachodzi taka prawidłowość. „Długie Odliczanie” jest oparte na okresie 360 dni, lub bardziej precyzyjnie na liczbach istniejących w numerycznym systemie Mayów. Widzimy tu prawdopodobną przyczynę odstępstwa przez Mayów od ścisłego systemu dwudziestkowego. System ten w  przybliżeniu reprezentował lata. Wiele napisów znaleziono w miastach Mayów, które opisywały daty ich założenia; oparte były na tym systemie liczbowym. Rozważmy dwa poprzednio wymienione przykłady liczbowe. Pierwszy przykład: [8; 14; 3; 1; 12]   jest datą wyrytą na kamiennej płycie  w mieście Tikal. Można to napisać jako: 12 + 1 x 20 + 3 x 18 x 20 + 14 x 18 x 20^2 + 8 x 18 x 20^3; co stanowi 1253912 dni od daty stworzenia świata, czyli 12 sierpnia 3113 p.n.e. Tak więc napis został wyryty w 320 r. n.e. Drugi przykład: [9; 8; 9; 13; 0]  jest datą ukończenia budynku w Palenque w Tabasco, w pobliżu miejsca przybycia Cortés’a. Można to napisać jako: 0 + 13 x 20 + 9 x 18 x 20 + 8 x 18 x 20^2 + 9 x 18 x 20^3; co stanowi 1357100 dni od daty stworzenia świata, czyli 12 sierpnia 3113 p.n.e. Tak więc napis został wyryty w 603 r. n.e.

Warto zauważyć niektóre właściwości (lub ściślej mówiąc niewłaściwości ) liczbowego systemu Mayów. Mayowie nie posługiwali się ułamkami, jednakże dokonywali bardzo precyzyjnych pomiarów astronomicznych. Ponadto, system Mayów nie był pełnym systemem dwudziestkowym i nie miał eleganckich matematycznych właściwości, które powinniśmy się spodziewać po systemie pozycyjnym. Na przykład: [9; 8; 9; 13; 0] = 0 + 13 x 20 + 9 x 18 x 20 + 8 x 18 x 20^2 + 9 x 18 x 20^3 = 1357100; jednakże [9; 8; 9; 13] = 13 + 9 x 20 + 8 x 18 x 20 + 9 x 18 x 20^2 = 67873.

 Przesuwając wszystkie liczby o jedno miejsce w lewo, pomnożyłoby liczbę przez 20 w prawdziwym dwudziestkowym systemie pozycyjnym, jednakże 20 x 67873 = 1357460, co nie równa się 1357100. Kiedy pomnożymy [9; 8; 9; 13] przez 20 otrzymujemy 9 x 400, natomiast w [9; 8; 9; 13; 0] mamy 9 x 360. Mayowie ponadto nie posiadali metody mnożenia i dzielenia liczb. Jednakże system liczbowy Mayów pozwalał na wykonywanie tych operacji. Jak wspomnieliśmy Mayowie mieli ustaloną stałą datę, tzw. data zero, inicjującą kalkulacje kalendarzowe. Data ta to 4 Ahau 8 Kumk, która w naszym gregoriańskim kalendarzu odpowiada 13 sierpnia 3113 p.n.e. Dni były pogrupowane na okresy podobnie jak nasze lata na wieki. Każdy okres miał specyficzny glif i nazwę:

Mayowie mieli sporą wiedzę o obrotach i cyklach astronomicznych ciał niebieskich, a w szczególności Słońca, Księżyca i Wenus.
Wykonywali pomiary astronomiczne ze zdumiewającą dokładnością, przy pomocy patyków stanowiących ich przyrządy pomiarowe. Używali dwa patyki ułożone w kształcie krzyża pod odpowiednim  kątem do obserwacji  obiektów astronomicznych. Budynek Caracaol w Chichen Itza był obserwatorium astronomicznym. Wiele okien w tym budynku jest tak umiejscowionych, aby pozwalały na obserwację określonych zjawisk na niebie jak np.: zachodzące słońce w czasie równonocy wiosennej.

Przy pomocy tak prymitywnych instrumentów Mayowie potrafili obliczyć długość roku równą 365,242 dni (rzeczywista wartość to 365,242198 dni). Inne niezwykłe obliczenia to długość miesiąca księżycowego.
W Copán (dzisiaj na granicy między Hondurasem a Gwatemalą) Mayowie odkryli, iż 149 miesięcy księżycowych trwa 4400 dni. Daje to 29,5302 dni jako długość miesiąca księżycowego. W Palenque w Tabasco obliczyli, iż 81 miesięcy księżycowych trwa 2392 dni. Daje to wynik 29,5308 dni jako długość miesiąca księżycowego. Dzisiejsza rzeczywista wartość wynosi 29,53059.
Czy to nie było niezwykłym osiągnięciem?