|
|
 |
Diofantos i algebra
Aleksandria przez wiele stuleci była centrum życia naukowego starożytnego świata. To tu powstała największa antyczna biblioteka (ok. 750 000 rękopisów). Działało tutaj wiele szkół, przyjeżdżało i kształciło się wielu uczonych. Aleksandria to miejsce, gdzie zdobyli swoje wykształcenie m.in. Archimedes, Euklides, Heron. To tu właśnie spędził całe swoje naukowe życie Diofantos (200/214 – 284/298 r. n.e.) - jeden z największych matematyków starożytności.
|
|
 |
 |
Diofantos z Aleksandrii jako pierwszy systematycznie zajął się algebrą, czyli teorią rozwiązywania równań. Wcześniej, jakkolwiek działania na liczbach i arytmetyka nie były Grekom obce, to pozostawały w ścisłym związku z geometrią, często matematyka wręcz utożsamiana była z geometrią. Nad wejściem do Akademii Platońskiej umieszczony był nawet napis: „Niech nie wchodzi tu nikt, kto nie zna geometrii”, gdzie geometria jest właśnie synonimem matematyki. Diofantos, zapewne dzięki kontaktom z uczonymi syryjskimi i hinduskimi, upowszechnił w nauce greckiej babilońskie zdobycze z dziedziny algebry. Trzeba również wspomnieć, że obowiązujące w Aleksandrii prawo nakazywało przyjezdnym zostawianie ksiąg do skopiowania i kopie te były następnie umieszczane w bibliotece. Sprzyjało to rozwojowi nauki i pozwalało zapoznać się z osiągnięciami naukowymi i literaturą wielu krajów. |
|
Główne dzieło Diofantosa to „Arytmetyka”. Składało się ono najprawdopodobniej z trzynastu ksiąg, z czego zachowało się sześć. Grecki matematyk przedstawił w swojej pracy 189 równań wraz z rozwiązaniami. Są to najczęściej równania nieoznaczone – to znaczy mające wiele rozwiązań – z jedną, dwiema bądź z trzema niewiadomymi. Diofantos narzucał na rozpatrywane równania takie warunki, aby rozwiązanie zawsze mieściło się w zbiorze liczb dodatnich i wymiernych. Rozważał co prawda zadanie sprowadzające się do równania 4x + 20 = 0, ale twierdził, że to równanie daje absurdalne rozwiązanie, liczby ujemne uważał za niedopuszczalne i je odrzucał. Rozwiązywał za to równania kwadratowe, układy równań kwadratowych, pisał o liczbach trójkątnych i kwadratowych oraz ustalał zależności między nimi.
Diofantos uważany jest za twórcę pierwszego, choć jeszcze bardzo niedoskonałego języka algebraicznego. Wprowadza odrębne symbole na oznaczenie niewiadomej, współczynniki pisze za niewiadomą, po raz pierwszy używa znaku odejmowania (odwrócona grecka litera psi – ψ), nie stosuje natomiast znaków dodawania, mnożenia i dzielenia. Składniki sum pisze obok siebie, używa za to skrótów słownych dla oznaczenia poszczególnych określeń i działań algebraicznych, np. ar – αρ (od słowa arithmos – liczba) na oznaczenie niewiadomej, is – ισ (od słowa isos – równy) na oznaczenie znaku „=”. Trzeba w tym miejscu dodać, że oryginalny zapis równań Diofantosa znacznie się różni od tego, który używany jest dziś przy przedstawianiu tych równań. Oprócz bowiem wymienionych wyżej skrótów trzeba by również uwzględnić grecki sposób zapisywania liter i cyfr (patrz tekst „Cyfrowa historia” – joński zapis liczb). Właśnie ze względu na bardzo skomplikowany zapis cyfrowy liczb i równań, jak twierdzą historycy matematyki, grecka arytmetyka rozwijała się tak bardzo powoli w porównaniu na przykład z arabską.
Do zasług Diofantosa w dziedzinie algebry zaliczyć trzeba też to, że jako pierwszy z matematyków greckich potraktował ułamki na równi z innymi liczbami, zapisywał je w ten sposób, że licznik stawiał nad mianownikiem, ale bez kreski ułamkowej. Rozwiązywanie przez Diofantosa równań polegało na ich sprowadzaniu do najprostszej postaci za pomocą przenoszenia wyrazów na drugą stronę równania ze zmienionym znakiem, redukcji wyrazów podobnych i dzieleniu przez współczynnik przy niewiadomej. Osiągnięcia Diofantosa przez wiele lat pozostały w zapomnieniu, wśród matematyków greckich nie znalazł on kontynuatorów. Jego dzieła przetrwały jednak w cytowaniach autorów arabskich i hinduskich i były przez nich bardzo cenione. W Europie jego „Arytmetykę” przetłumaczono z arabskiego dopiero w epoce nowożytnej i od razu wzbudziła zainteresowanie i zajęła stałe miejsce w historii matematyki. To właśnie na marginesie książki Diofantosa Pierre de Fermat zapisał swoje słynne twierdzenie znane jako wielkie twierdzenie Fermata, które do dziś wywołuje dyskusje. Do dzieła Diofantosa nawiązywało wielu wybitnych matematyków, m.in.: wspomniany już Pierre de Fermat, Leonhard Euler, Joseph Lagrange.
ZADANIA DIOFANTOSA
I
Liczby trójkątne, kwadratowe, sześcienne – ich obliczanie i ustalanie wzajemnych powiązań jest bardzo charakterystyczne dla matematyki w starożytnej Grecji. Diofantos również odkrył wiele prawidłowości rządzących liczbami. Jedno z jego twierdzeń mówi: „Ośmiokrotnie wzięta liczba trójkątna powiększona o jedność jest zawsze kwadratem”; inaczej mówiąc: ośmiokrotnie wzięta liczba trójkątna powiększona o jedność jest zawsze liczbą kwadratową. Aby więc lepiej wyjaśnić to twierdzenie, należy poznać, co to są liczby trójkątne i liczby kwadratowe.
Liczba trójkątna to każda taka liczba o numerze n, będąca na przykład liczbą kół jednakowej wielkości, z których można ułożyć trójkąt równoboczny o boku zbudowanym z n kół. Graficznie liczby trójkątne można przedstawić następująco:
|
|
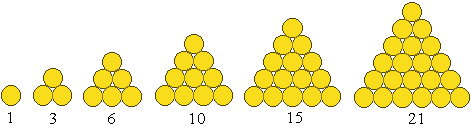 |
Zależność na n-tą liczbę trójkątną można przedstawić według wzoru:
|
|
gdzie n jest liczbą naturalną. Liczba trójkątna o n-tym numerze jest sumą kolejnych liczb naturalnych.
Liczba kwadratowa natomiast to każda taka liczba o numerze n, będąca na przykład liczbą kół jednakowej wielkości, z których można ułożyć kwadrat o boku zbudowanym z n kół. Graficznie liczby kwadratowe można przedstawić następująco:
|
|
Zależność na n-tą liczbę kwadratową można przedstawić według wzoru:
|
|
gdzie n jest liczbą naturalną. Liczby kwadratowe są więc kwadratami kolejnych liczb ciągu naturalnego.
Na podobnej zasadzie jak liczby trójkątne i kwadratowe tworzone są inne liczby wielokątne. Przykłady liczb trójkątnych, kwadratowych i innych wielokątnych przedstawia tabela:
|
|
Twierdzenie Diofantosa, że ośmiokrotnie wzięta liczba powiększona o jedność jest zawsze kwadratem, pokazuje poniższy rysunek:
|
|
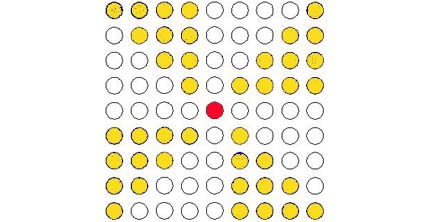 |
Za pomocą twierdzenia Diofantosa można sprawdzić, czy dana liczba jest trójkątna. Weźmy na przykład 45 i sprawdźmy, czy jest to liczba trójkątna. Korzystając z twierdzenia Diofantosa, otrzymujemy: 8 ∙ 45 + 1 = 361, a liczba 361 jest liczbą kwadratową, bo 19 ∙ 19 = 361, stąd wniosek, że liczba 45 jest liczbą trójkątną.
II
Diofantos ułożył następujące zadanie: suma dwóch liczb wynosi 100, a ich różnica 40 – jakie to liczby?
Oznaczamy: x – mniejsza liczba; y – większa liczba
Mamy układ równań: x + y = 100 i y - x = 40
x + y = 100 i po przekształceniu drugiego równania: y = 40 + x
Do pierwszego równania w miejsce y wstawiamy 40 + x i otrzymujemy:
x + 40 + x = 100
2x = 60
x = 30
y = 40 + 30
y = 70
III
Diofantos podał i rozwiązał następujące zadanie: „Znaleźć takie trzy liczby, których suma, a także suma każdej pary tych liczb jest kwadratem innej liczby”. Grecki matematyk znalazł te liczby. Są to 80, 320 i 41. Ich suma rzeczywiście jest kwadratem, bo 80 + 320 + 41 = 441 = 21². Suma każdej pary tych liczb jest również kwadratem: 80 + 41 = 121 = 11², 320 + 41 = 361 = 19², 320 + 80 = 400 = 20².
Jak Diofantos znalazł te liczby? Nazwał szukane liczby a, b, c. Operował tylko jedną niewiadomą x. Następnie założył, że:
a + b + c = x² + 2x + 1 = (x + 1)²
a + b = x²
b + c = x² - 2x + 1 = (x - 1)²
Z tych równań wyznaczył a = 4x oraz c = 2x + 1, skąd a + c = 6x + 1
Biorąc pod uwagę, że a + c jest kwadratem innej liczby, znalazł, że x może mieć wartość tylko 20.
Z powyższych równań wynika więc, że:
a = 4x = 80
b = x² - a = 400 - 80 = 320
c = 2x + 1 = 40 + 1 = 41
|
|
ZAGADKA – ILE LAT ŻYŁ DIOFANTOS?
W XIV wieku grecki mnich Maksymus Planudes umieścił w swojej antologii wiersz „Epitafium Diofanta”. Jego treść jest jednocześnie zadaniem tekstowym:
Pod tym nagrobkiem spoczywa Diofant – a dzięki przedziwnej
Sztuce zmarłego i wiek zdradzi ci ten głaz:
Chłopcem przez szóstą część życia pozostać bóg mu pozwolił,
Lica pokwitły mu zaś, kiedy dwunasta znów część
Życia minęła; a znowu żywota gdy przebył część siódmą,
Młodą małżonkę w dom dobry wprowadził mu bóg,
Która, gdy pięć lat minęło, małego powiła mu synka,
Ale okrutny chciał los, że kiedy syn ledwie wiek
Ojca w połowie osiągnął, ponury zabrał go Hades.
Kojąc ogromny swój ból, szukał Diofant wśród liczb
Jeszcze przez cztery lata pociechy, aż rozstał się z życiem.
ROZWIĄZANIE
x – czas życia Diofantosa
1/6x – jego dzieciństwo
1/12x – okres młodości
1/7x – czas między wiekiem młodzieńczym a ślubem
5 – lata oczekiwania na syna
1/2x – czas życia syna
4 – czas, jaki Diofantos żył po śmierci syna
Rozwiązanie zadania polega na ułożeniu prostego równania z jedną niewiadomą:
1/6x + 1/12x + 1/7x + 5 + 1/2x + 4 = x
Stąd po wykonaniu prostych działań otrzymujemy x = 84, czyli Diofantos żył 84 lata.
|
|
|
 |
|

