|
|
 |
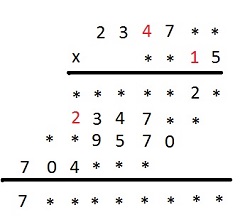
Zwróćmy uwagę, że w iloczynie cząstkowym liczba powstała z mnożenia, przez drugą cyfrę mnożnika, ma tyle cyfr co mnożna i cyfry 3 i 7 się powtarzają i są na tych samych pozycjach. Oznacza to, że cyfrą dziesiątek w mnożniku będzie 1 a cyfrą tysięcy w mnożnej będzie 4.
|
 |
 |
|
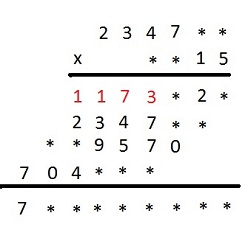
Mnożąc mnożną przez 5 odkryjemy cztery początkowe cyfry pierwszego iloczynu cząstkowego.
|
 |
 |
|
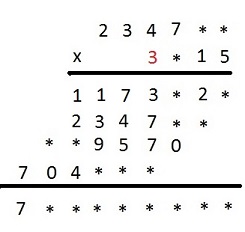
Z odkrytych już cyfr widać, że ostatni iloczyn częściowy jest trzy razy większy od mnożnej. Oznacza to, że cyfrą tysięcy mnożnika jest 3.
|
 |
 |
|
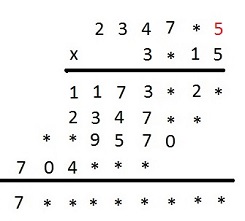
Ponieważ trzeci iloczyn częściowy ma tyle cyfr co mnożna, więc w rzędzie setek mnożnika, musi być cyfra mniejsza niż 5. Napewno nie będzie to cyfra 3, bo wówczas w rzędzie tysięcy iloczynu częściowego była by cyfra 4, a jest cyfra 9. Pozostaje, więc cyfra 2 albo 4, co oznacza, że cyfrą jedności mnożnej jest cyfra 5.
|
 |
 |
|
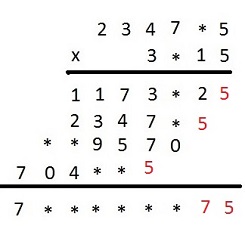
Pozwala to odkryć następne cyfry mnożenia.
|
 |
 |
|
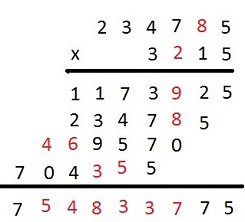
Z analizy trzeciego iloczynu cząstkowego wynika, że cyfrą setek mnożnika jest 2, a cyfrą dziesiątek mnożnej 8. Możemy teraz odtworzyć całe mnożenie.
|
 |
 |
|
|
 |
|

