Widać, że jeden czynnik mnożenia jest trzycyfrowy, a drugi dwucyfrowy. Sprawdźmy jaka największa liczba trzy cyfrowa pomnożona przez dwucyfrową da iloczyn czterocyfrowy. Podzielmy więc liczbę czterocyfrową przez dwucyfrową. Aby iloraz był jak największy, należy dzielną wybrać możliwie  największą, a dzielnik możliwie najmniejszy.
Największą liczba  czterocyfrowa spełniająca te warunki to 9988. Najmniejsza liczba dwucyfrowa spełniająca nasze warunki to 20, 9988/20=499,4 czyli NPP<500. Ponieważ w rzędzie setek jest liczba nieparzysta,

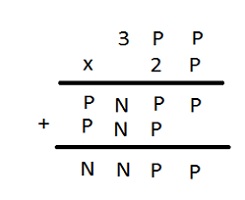
więc pierwsza cyfra dłuższego czynnika może być 1 albo 3. Ponieważ pierwszy iloczyn częściowy, który powstał z pomnożenia trzycyfrowego czynnika  przez parzystą liczbę jednocyfrową ma cztery cyfry i rozpoczyna się cyfrą parzystą czyli jest większy od 2000 więc 1 odpada pozostaje tylko 3. Ponieważ drugi iloczyn częściowy jest trzycyfrowy i powstał z przemnożenia liczby trzycyfrowej przez parzystą liczbę jednocyfrową, więc ta liczba jednocyfrowa musi być mniejsza od 4 czyli wynosi 2. Uwzględniając te spostrzeżenia mamy

Aby czterocyfrowa liczba stojąca w trzecim rzędzie była większa od 2100 (rozpoczyna się liczbą parzystą) pod pozostałym w drugim czynniku P musi ukrywać się cyfra 6 albo 8.
Ponieważ  trzycyfrowa liczba stojąca w czwartym rzędzie rozpoczyna się cyfrą parzystą, więc 2 pomnożone przez środkowe P z pierwszej trzycyfrowej liczby musi być jednocyfrowe, czyli pod tym P może ukrywać się 0; 2 lub 4.
Gdyby pod P w liczbie dwucyfrowej schowane było 6, wówczas albo liczba z trzeciego rzędu była mniejsza od 2000, albo pod N ukrywało by się 0, co nie spełnia warunków zadania, czyli  drugi czynnik to 28.

Drugie P przemnożone przez 8 musi dać przeniesienie do rzędu setek, więc nie może być 0. Pierwsze P też musi po przemnożeniu przez 2 dać przeniesienie do rzędu dziesiątek w liczbie stojącej w czwartym rzędzie więc może wynosić 6 albo 8.
Pozostały do sprawdzenia 4 iloczyny: 326 * 28; 328 * 28; 346 * 28 i 348 * 28.
Poprawne rozwiązanie to 348 *28