|
|
 |
Najpiękniejsze wzory matematyczne |
|
Jedną z podstawowych umiejętności matematycznych, jest umiejętność opisywania praw matematycznych i przyrodniczych za pomocą równań i wzorów matematycznych. Niektóre z tych wzorów stanowią już klasykę. Znane są niemalże wszystkim, nie tylko matematykom. Jedni podziwiają ich prostotę, inni ich piękno, jeszcze inni poetyckie prawdy jakie zawierają.
Oto kilka najbardziej znanych wzorów.
|
|
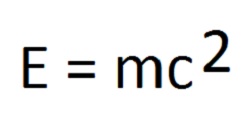 |
 |
Ten najsłynniejszy chyba wzór fizyczny świata jest dla wielu niemal symbolem nowoczesnej fizyki, albo prawie obiektem religijnego zafascynowania.
Masa.. Energia?... Jedno równe drugiemu. I jeszcze ta prędkość światła – c – jedna z najbardziej tajemniczych stałych fizycznych. |
|
Klasyczne wspaniałe równanie to słynne równanie Pitagorasa, który zna każdy uczeń.
Wzór odkryty przez Leonharda Eulera podający zależność między ilością ścian, krawędzi i wierzchołków dowolnej bryły.
Jeżeli w wielościanie wyodrębnimy wszystkie ściany, krawędzie oraz wierzchołki, oraz niech F będzie ilością wszystkich ścian badanego wielościanu, E – ilością krawędzi oraz V - ilością wierzchołków, to zawsze otrzymamy zależność: V – E + F = 2. Jeżeli na przykład weźmiemy czworościan, mający: cztery ściany, będące trójkątami, sześć krawędzi oraz cztery wierzchołki, to widzimy, że V – E + F = 2. To samo dotyczy ostrosłupa (piramidy) z pięcioma płaszczyznami – cztery trójkątne oraz jeden kwadrat – ośmioma krawędziami oraz pięcioma wierzchołkami, oraz również dowolnej innej kombinacji płaszczyzn, krawędzi i wierzchołków.
|
|
Definicja całki Izaaka Newtona
|
|
Rachunek różniczkowy i całkowy – dział matematyki zajmujący się badaniem funkcji zmiennej rzeczywistej lub zespolonej w oparciu o podstawowe dla tej dyscypliny matematycznej pojęcia pochodnych i całek. Rachunek różniczkowy jest jednym z podstawowych narzędzi matematycznych fizyki i techniki.
Rachunek różniczkowy i całkowy rozwinął w XVII wieku Izaak Newton, który przy ich pomocy opisał ruch planet wokół Słońca.
WZÓR EULERA
|
|
Wzór ten porównuje się z sonetami Szekspirowskimi i uważany jest za najpiękniejszy wzór matematyczny.
W powyższym równaniu wykorzystano trzy działania arytmetyczne: dodawanie, mnożenie i potęgowanie. Co więcej, zawiera ono pięć najważniejszych stałych matematycznych, użytych jednokrotnie: 0, 1, pi, e, i. Ponadto lewa strona równa jest prawej, wzór jest prawdziwy! |
 |
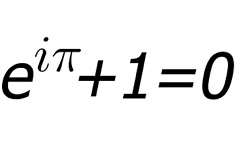 |
|
Wyjaśnienie:
0 – to najciekawsza liczba rzeczywista, element neutralny dodawania.
1 – Element neutralny mnożenia, w informatyce symbol prawdy.
pi – liczba niewymierna, definiowana jako stosunek długości okręgu do długości średnicy tego okręgu, w przybliżeniu 3,1415.
e – podstawa logarytmu naturalnego w przybliżeniu wynosi 2,7182.
i – jednostka urojona liczby zespolonej. |
|
Twórcą bardzo wielu charakterystycznych równań, które stały się symbolem współczesnej fizyki jest Albert Einstein, twórca teorii względności.
Oto próbki jego efektownych wzorów:
Ogólna teoria względności
|
|
Wzór wiąże geometrię czasoprzestrzeni z rozkładem materii
|
|
Szczególna teoria względności
|
|
Wzór opisuje zależność wydłużania i skracania się czasu względem prędkości z jaką porusza się obserwator..
|
 |
 |
|
 |
 |
Prosta zależność między liczbą 1 a jej rozwinięciem nieskończonym okresowym.
|
|
Równanie minimalnej powierzchni.
|
|
Równanie opisuje powierzchnię baniek mydlanych rozpiętych na drucianych ramkach.
Równanie Callan-Symanzik
|
|
Za pomocą tego równania fizycy obliczają masę i rozmiar protonów i neutronów wchodzących w skład jądra atomu.
|
|
|
 |
|

