|
|
 |
Liczby pitagorejczyków
Galileusz twierdził, że „księga przyrody napisana jest w języku matematyki”. Pitagorejczycy nie dość, że byli pierwszymi, którzy już dużo wcześniej głosili podobny pogląd, to jeszcze rozszerzyli go na wszystkie dziedziny rzeczywistości. Ich mottem było: „Liczba jest istotą wszystkich rzeczy”.
|
|
 |
 |
Twórcą związku pitagorejskiego był Pitagoras z Samos (ok. 570 r. p.n.e. - 497 r. p.n.e.). Założona przez niego szkoła w Krotonie (południowe Włochy, wówczas kolonia grecka) miała charakter filozoficzno-religijny. Była to jednak religia i filozofia bardzo szczególna, oparta w znacznym stopniu na matematyce. Pitagorejczycy głosili bowiem pogląd, że cała rzeczywistość zawiera w sobie matematyczną harmonię. Jej odkrycie i opisanie stanowiło podstawowy cel ich dociekań. Dlatego też jako pierwsi rozpoczęli systematyczne prace w dziedzinie matematyki mające charakter teoretyczny. |
|
| Wcześniej bowiem zajmowano się matematyką od strony praktycznej, gdy trzeba było na przykład dokonać pomiarów w terenie czy podczas wznoszenia budowli. Jak napisał o nich Arystoteles: „Tak zwani pitagorejczycy zajęli się pierwsi matematyką i pchnęli ją naprzód”. Ich wkład w rozwój matematyki w głównej mierze polegał na odkrywaniu i uzasadnieniu teoretycznym twierdzeń matematycznych, ale był też wypadkową dociekliwości, genialnej intuicji, a nawet wręcz zabawy liczbami.
Twierdzenie Pitagorasa i odcinki niewspółmierne
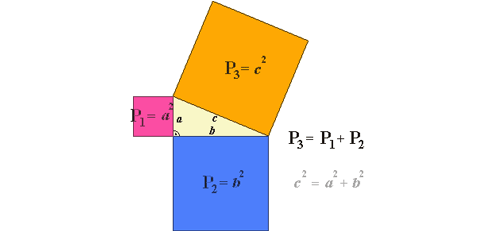
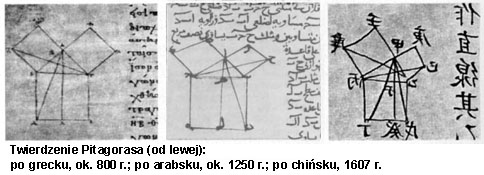
Jednym z najbardziej znanych i znaczących osiągnięć szkoły pitagorejskiej jest twierdzenie Pitagorasa. Sama nazwa może być jednak myląca, ponieważ nie można z całą pewnością stwierdzić, czy autorem tego twierdzenia był Pitagoras. Nie zachowały się bowiem żadne jego pisma, a częstą praktyką było w tamtych czasach powoływanie się uczniów na autorytet mistrza. Nie ulega jednak wątpliwości, że dowód twierdzenia powstał w szkole pitagorejskiej. Twierdzenie Pitagorasa głosi, że: jeżeli trójkąt jest prostokątny, to kwadrat długości przeciwprostokątnej jest równy sumie kwadratów długości przyprostokątnych. Prawdziwe jest również twierdzenie odwrotne: jeżeli w trójkącie suma pól kwadratów zbudowanych na dwóch krótszych bokach jest równa polu kwadratu zbudowanego na najdłuższym boku, to trójkąt jest prostokątny. Graficznie twierdzenie Pitagorasa można przedstawić w następujący sposób:
|
|
 |
Kolejnym ważnym osiągnięciem pitagorejczyków jest twierdzenie o sumie wszystkich kątów w trójkącie, która wynosi 180 stopni. Jako pierwsi w swoich pracach wprowadzili lub zdefiniowali oni również takie terminy, jak: elipsa, parabola, hiperbola, punkt, prosta, odcinek. Największe konsekwencje dla rozwoju związku pitagorejskiego pociągnęło za sobą odkrycie liczb niewymiernych. Nastąpiło to podczas badania kwadratu. Odkryto wówczas, że bok i przekątna kwadratu są odcinkami niewspółmiernymi, czyli takimi, których nie można wyrazić za pomocą ułamka zwykłego o całkowitym liczniku i mianowniku, nie mają wspólnej miary. Inaczej mówiąc – jeśli liczba wymierna jest długością boku kwadratu, to żadna liczba wymierna nie jest długością jego przekątnej. Przekątna kwadratu ma długość a√2, gdzie a jest długością boku kwadratu, natomiast √2 jest liczbą niewymierną, nie można jej przedstawić za pomocą ułamka, którego licznik i mianownik są liczbami całkowitymi, podobnie jak liczby π. Nazwano je wówczas liczbami niewyrażalnymi - alogoj. Odkrycie liczb niewymiernych, wcześniej przez Greków nieznanych, początkowo zachwiało głoszoną przez pitagorejczyków wiarą w świat harmonijny, pełen proporcji, mierzalny za pomocą liczb i dający się opisać za pomocą figur geometrycznych. Najpierw fakt odkrycia liczb niewymiernych związek pitagorejski trzymał w tajemnicy, później jednak nastąpił podział szkoły na akuzmatyków i matematyków. Ci pierwsi porzucili dociekania matematyczne i obrali drogę religijno-etyczną, kontemplacyjną i mistyczną. Matematycy natomiast, nie porzucając religii, opowiedzieli się za koniecznością dalszego prowadzenia studiów naukowych i zajmowali się przede wszystkim geometrią.
|
|
 |
Wszystko jest liczbą
Niespodziewane odkrycie liczb niewymiernych i spowodowane tym faktem wątpliwości co do sensu i możliwości prowadzenia badań w tym zakresie nie doprowadziły jednak do odrzucenia przez pitagorejczyków poglądu, że światem rządzą liczby. Nawet wręcz przeciwnie – zaczęto dostrzegać jeszcze bardziej tajemnicę i siłę liczb oraz podkreślać ich mistyczny charakter. Bez obecności liczb wszystko byłoby bezkresne, niepojęte, chaotyczne. To liczby kształtują rzeczywistość i poprzez odkrywanie ich obecności w świecie możliwe jest wszelkie poznanie. Pitagorejczycy rozumieli liczby nie jako abstrakcje, lecz przypisywali im przestrzenną wielkość i realny kształt. Liczby kwadratowe, trójkątne czy sześcienne swą nazwę zawdzięczają własnościom odkrytym podczas badania figur geometrycznych – kwadratów, trójkątów, sześcianów. Konsekwencją poglądu o obecności liczb we wszystkich rzeczach była metoda poznania, polegająca na odkrywaniu, porównywaniu i zestawianiu liczb.
|
|
 |
 |
Głównym osiągnięciem szkoły pitagorejskiej w dziedzinie arytmetyki było dokonanie przez nią po raz pierwszy klasyfikacji liczb, zaczęto je systematycznie badać. Zostały one podzielone na parzyste i nieparzyste; będące kwadratami (4, 9, 16, 25, 36, ...) i niebędące kwadratami (2, 3, 5, 6, 7, ...). Ponadto wyróżniano liczby doskonałe (6, 28, 496, 8128, ...), czyli takie, które są równe sumie swoich dzielników mniejszych od samej liczby, np. 6 = 1 + 2 + 3; 28 = 1 + 2 + 4 + 7 + 14.
Pitagoras miał również wymyślić definicję słowa „przyjaźń”. Na pytanie, kto to jest przyjaciel, odpowiedział: „Ten, który jest drugim ja, tak jak 220 i 284”. |
|
Zostały w ten sposób utworzone liczby zaprzyjaźnione, czyli pary liczb, w których suma dzielników jednej liczby daje drugą i odwrotnie (220 i 284; 1184 i 1210; 5020 i 5564; 6232 i 6368; 9363584 i 9437056, ...), np. suma dzielników liczby 220: 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284, a suma dzielników liczby 284: 1 + 2 + 4 + 71 + 142 = 220.
Pitagorejczycy zajmowali się również problemem harmonii muzycznej i głosili pogląd, że powstaje ona dzięki liczbie i da się przez liczby wyrazić, byli twórcami kwintowej skali muzycznej. Odkryli oni, że dźwięki muzyczne wykazują matematyczną prawidłowość i że ich przyczyną jest ruch. Swoje badania prowadzili, wykorzystując monochord – jednostrunowy przyrząd muzyczny. Za pomocą przesuwanego mostka skracano strunę monochordu tak, aby stosunki długości jej odcinków były liczbami całkowitymi, i otrzymano trzy interwały: oktawę (1:2), wyrażającą stosunek połowy do całości, kwintę (2:3) i kwartę (3:4). Za pomocą dodawania i odejmowania tych interwałów można było uzyskać pozostałe dźwięki. Nietrudno dostrzec, że suma liczb 1, 2, 3, 4 daje 10 – liczbę wyrażającą doskonałość według wierzeń pitagorejskich.
Spekulacje liczbowe i genialna intuicja
Wiele badań pitagorejczyków miało charakter spekulacji liczbowych, nadawano liczbom znaczenie symboliczne i przypisywano im różne własności. Tak na przykład: 1 oznaczała punkt; 2 – linię; 3 – płaską figurę geometryczną; 4 – ciało geometryczne; 5 – własności ciał fizycznych; 6 – życie; 7 – ducha; 8 – miłość; 9 – roztropność i sprawiedliwość; 10 – doskonałość wszechświata. Ta sama liczba mogła również symbolizować kilka pojęć, np. 1 oznaczała monadę, matkę wszystkich liczb, ale także środek wszechświata; 5 oznaczło również zdrowie. Podstawowa zasada pitegorejczyków „wszystko jest liczbą” nie miała więc żadnych wyjątków co do zakresu jej stosowania.
Największe znaczenie, wykraczające daleko poza krąg szkoły pitagorejskiej, miały jednak osiągnięcia dotyczące astronomii, na które powoływali się 2000 lat później Mikołaj Kopernik i Johannes Kepler. Były one możliwe zarówno dzięki wyciąganiu trafnych wniosków z obserwowanych zjawisk przyrodniczych, jak i w dużej mierze intuicyjnego szukania i proponowania rozwiązań, bardzo często sprzecznych z ówcześnie panującymi teoriami i poglądami. Pitagorejczycy po raz pierwszy wysunęli tezę o kulistości Ziemi, wynikającą z obserwacji wcześniejszego pojawiania się gwiazd na niebie na Wschodzie. Kulę uważali ponadto za najdoskonalszą i najprostszą bryłę, co jeszcze bardziej umocniło ich pogląd. Przełomowy poznawczo był jednak fakt, że prawdziwy kształt Ziemi nie musi być wcale oglądany zmysłami, można go ująć jedynie za pomocą myśli matematycznej.
|
|
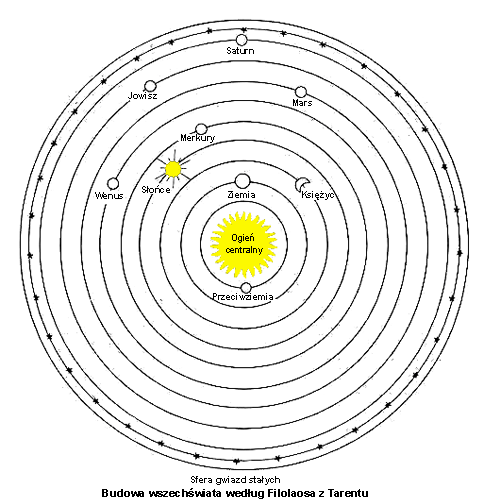 |
W dalszych rozważaniach astronomicznych pitagorejczycy wyróżnili również dziewięć sfer mających formę koncentrycznych kul, do których przytwierdzone są ciała niebieskie: Ziemia, Słońce, Księżyc, 5 planet, które znali (Wenus, Mars, Saturn, Jowisz, Merkury), i sfera gwiazd stałych. Jako że sfer było 9, a liczbą doskonałą była 10, twierdzili, iż zgodnie z zasadą pełnej harmonii i doskonałości wszechświata musi istnieć jeszcze jedna sfera, określana później przez niektórych pitagorejczyków, m.in. Filolaosa z Tarentu, jako Antychton – Przeciwziemia. Jedna z koncepcji pitagorejskich głosiła, że Ziemia stanowi punkt centralny wszechświata, wokół którego krążą pozostałe sfery, dopuszczano przy tym, że Ziemia może krążyć dookoła swej osi i tym tłumaczono zjawiska atmosferyczne. Pojawiały się jednak i inne próby uporządkowania kosmosu. Filolaos z Tarentu usunął Ziemię z centrum i umieścił tam wieczny ogień z krążącymi wokół niego sferami, łącznie z Ziemią. Słońce i Księżyc miałyby tylko odbijać światło pochodzące od wiecznego ognia. Te dwie koncepcje – ruchu obrotowego i obiegowego Ziemi przez żadnego z pitagorejczyków nigdy nie były rozpatrywane łącznie, na to trzeba było poczekać aż do czasów nowożytnych.
(dt) |
|
|
 |
|

