|
|
 |
Parametryczne równanie kartezjańskie:
x = (a + b) cos(t) – b cos((a/b + 1)t), y = (a + b) sin(t) – b sin((a/b + 1)t)
|
|
Istnieją cztery krzywe blisko powiązane ze sobą. Są to epicykloida, epitrochoida, hipocykloida oraz hipotrochoida. Wykreślane są przez punkt P leżący na obwodzie okręgu o promieniu b, który toczy się wokół po obwodzie nieruchomego okręgu o promieniu a.
Dla wyżej pokazanej epicykloidy, okrąg o promieniu b toczy się na zewnątrz okręgu o promieniu a. Punkt P znajduje się na okręgu o promieniu b. Dla powyższego przykładu a = 8 oraz b = 5. Gdy a = 2b, wtedy otrzymamy krzywą w kształcie nerki.
Krzywe niniejsze badali: Dürer (1525), Desargues (1640), Huygens (1679), Leibniz, Newton (1686), de L’Hopital (1690), Jacob Bernoulli (1690), la Hire (1694), Johan Bernoulli (1695), Daniel Bernoulli (1725), Euler (1745, 1781).
Jeżeli a = (m - 1)b, gdzie m jest liczbą całkowitą, wtedy długość epicykloidy wynosi 8mb, a jej powierzchnia równa się  b2(m2 + m). b2(m2 + m).
Kształt epicykloidy zależy od stosunku R/r promieni okręgów nieruchomego do toczącego się. W przypadku, gdy stosunek ten jest równy 1 otrzymujemy kardioidę, zwaną również ze względu na charakterystyczny kształt krzywą sercową. Epicykloida jest szczególnym przypadkiem epitrochoidy.
|
|
Powstawanie kardioidy gdy R/r = 1
|
 |
Epicykloida gdy R/r=3 |
|
Jeżeli stosunek R/r jest liczbą niewymierną, otrzymujemy krzywą otwartą. Kolejne przybliżenia takiej sytuacji pokazują poniższe rysunki:
R/r – niewymierne
|
|
Niektórzy matematycy definiują tę spiralę jako związek krzywych
r = ψ oraz r = - ψ.
|
|
Odległość pomiędzy kolejnymi zwojami jest stała, ponieważ istnieje liniowa relacja pomiędzy kątem a promieniem.
Spirale od wieków fascynowały matematyków. Archimedes (287 - 212 p.n.e.) napisał traktat o spiralach, a jedna z nich została nawet nazwana jego imieniem. Spirala Archimedesa jest dobrym modelem rowka na płycie gramofonowej lub krawędzi zwiniętego dywanu. Cechą charakterystyczną spirali Archimedesa jest to, że odległość pomiędzy zwojami jest wszędzie taka sama. Matematyczny model takiej spirali jest łatwy do opisania, jeśli tylko przejdziemy do współrzędnych biegunowych: punkt na płaszczyźnie o współrzędnych kartezjańskich (x, y) będzie wtedy wyznaczony przez dwie liczby (r, ψ), gdzie r jest odległością od środka układu współrzędnych (promieniem wodzącym), a ψ jest kątem pomiędzy promieniem r, a dodatnią półosią x, mierzonym w radianach. A zatem x = r cos(ψ) i y = r sin(ψ).
Przy tym opisie spirala Archimedesa (widziana ze swojego środka) może być wyznaczona przez równanie: r=q ψ gdzie ψ jest dowolną liczbą nieujemną. W szczególności ψ = 2δ oznacza jeden obrót, y = 4δ dwa obroty itd. Rysowanie spirali zaczynamy od środka. W czasie, gdy ψ wykona jeden pełny obrót, promień wzrośnie o 2δq - stałą odległość między kolejnymi zwojami.
Krzywa może być użyta do zamiany jednostajnego ruchu kątowego na jednostajny ruch liniowy: należy w tym celu zbudować krzywkę zawierającą dwie odgałęzienia krzywej spirali. Obracając krzywkę ze stałą prędkością wokół jego środka pozwala uzyskać jednolity ruch liniowy.
Właściwość ta była wykorzystywana w starszych modelach maszyn do szycia. W przyrodzie niniejszą krzywę można ujrzeć odwzorowaną na szyszkach sosnowych. Niektóre amonity mają formę spirali Archimedesa; większość jednak zbudowana jest zgodnie ze spiralą logarytmiczną.
W spirali Archimedesa wzrost polega tylko na dodawaniu, w przeciwieństwie do spirali logarytmicznej, której wzrost uzależniony jest od jej rozmiaru.
Odwrotność spirali Archimedesa stanowi spirala hiperboliczna, a konchoida spirali stanowi również spiralę Archimedesa.
|
|
Spiralę Archimedesa można zobaczyć na ekranie komputera zarażonego wirusem win32.hybris. Ten robak e-mailowy potrafi rozszerzyć swoją funkcjonalność używając plugi'ny; jeden z plugin'ów pokazuje spiralę Archimedesa na monitorze, którą nie można zamknąć.
|
 |
 |
|
Spirala Archimedesa używana jest m.in. do rozwiązywania jednego ze słynnych problemów delijskich, mianowicie zagadnienia kwadratury koła (chodzi o konstrukcję kwadratu o polu równym polu danego koła). Jeśli używamy wyłącznie środków klasycznych, tj. cyrkla i linijki, jest to problem nierozwiązywalny, natomiast skorzystanie ze spirali Archimedesa umożliwi skonstruowanie żądanego kwadratu.
Spiralami niezbyt ściśle przyjęto nazywać krzywe płaskie, charakteryzujące się tym, że we współrzędnych biegunowych ich promień wodzący zależy od kąta monotonicznie (czyli rosnąco lub malejąco). W przypadku spirali Archimedesa promień jest wprost proporcjonalny do kąta. Oznacza to, że mówiąc obrazowo jeśli mucha startująca ze środka wirującej płyty gramofonowej będzie poruszała się ze stałą szybkością ku brzegowi po promieniu, to zatoczy spiralę Archimedesa.
|
|
 |
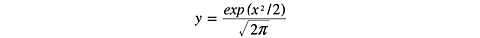 |
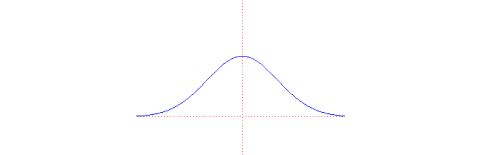
Niniejszą krzywę, zwaną teź krzywą błędu, po raz pierwszy zbadał de Moivre w 1733 roku. Następnymi badaczami tej krzywej byli Laplace oraz Gauss, dlatego krzywa ta nazywa się również krzywą Gaussa.
Rozkład normalny, zwany też rozkładem Gaussa, lub krzywą dzwonową, jest jednym z najważniejszych rozkładów prawdopodobieństwa. Odgrywa ważną rolę w statystycznym opisie zagadnień przyrodniczych, przemysłowych, medycznych, socjalnych itp.
Przyczyną jest jego popularność w naturze. Jeśli jakaś wielkość jest sumą lub średnią bardzo wielu drobnych losowych czynników, to niezależnie od rozkładu każdego z tych czynników, jej rozkład będzie zbliżony do normalnego. Ponadto rozkład normalny ma interesujące właściwości matematyczne, dzięki którym oparte na nim metody statystyczne są dość proste obliczeniowo.
Błędy pomiaru. Wielokrotne powtarzanie tego samego pomiaru daje wyniki rozrzucone wokół określonej wartości. Jeśli wyeliminujemy wszystkie większe przyczyny błędów, zakłada się, że pozostałe mniejsze błędy muszą być rezultatem dodawania się do siebie dużej liczby niezależnych czynników, co daje w efekcie rozkład normalny. Odchylenia od rozkładu normalnego rozumiane są jako wskazówka, że zostały pominięte błędy systematyczne. To stwierdzenie jest centralnym założeniem teorii błędów.
|
|
Równanie kartezjańskie: x2/a2 - y2/b2 = 1
|
|
Euklides oraz Aristeusz napisali pracę o hiperboli, lecz omówili tylko jedno jej odgałęzienie. Oba rozgałęzienia po raz pierwszy zostały zbadane przez Apoloniusza, natomiast ognisko oraz kierownicę omówił Pappus.
Ewoluta hiperboli o powyższym równaniu stanowi krzywa Lamé’go
Hiperbola jest to krzywa stożkowa, będąca zbiorem punktów takich, że wartość bezwzględna różnicy odległości tych punktów od dwóch punktów, nazywanych ogniskami hiperboli, jest stała.
|
|
|
 |
|

