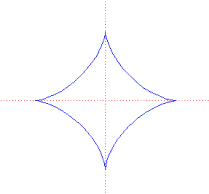
ASTEROIDA
  

   Asteroida powstaje gdy mniejszy okrąg toczy się bez poślizgu wewnątrz i wokół większego, zewnętrznego okręgu. Punkt na obwodzie małego okręgu zakreśla asteroidę, gdy stosunek R/r promieni okręgów dużego do małego jest równy 4.
   Jeżeli stosunek ten wynosi 3 wtedy otrzymujemy hipocykloidę z trzema ostrzami.
   Dla R/r = 2 hipocykloida redukuje się do prostej linii – średnicy dużego okręgu – fakt ten jest znany jako twierdzenie Kopernika i może być wykorzystany do zamiany ruchu obrotowego na posuwisto-zwrotny.
 

Równanie kartezjańskie: 

x^2/3 + y^2/3 = a^2/3;

gdzie a jest ustaloną liczbą rzeczywistą.

Układ równań parametrycznych:  x = a cos³(t),  y = a sin³(t)
 

 
   Krzywa była badana przez Jakuba Bernoulliego w latach 1691-1692. Pojawiła się również wzmianka o niej w listach Leibniza z roku 1715. Obecną nazwę otrzymała w roku 1836, ale jeszcze długo występowała w literaturze fachowej pod innymi nazwami: kubocykloidy lub tetrakuspidy.
   Długość obwodu asteroidy o parametrze a wynosi 6a, gdzie a jest promieniem okręgu opisanego na asteroidzie. Zamknięta nią powierzchnia równa jest 3a²/8. Powyżej pokazano asteroidę o a = 3.
   Pole powierzchni obrotowej powstałej z obrotu asteroidy dokoła osi symetrii przechodzącej przez jej wierzchołki ma wartość 12a²/5, natomiast objętość bryły ograniczonej tą powierzchnią wynosi 32a³/105.
 

 
KARDIOIDA czyli krzywa sercowa
 

   Kardioida (krzywa sercowa) – krzywa opisana przez ustalony punkt okręgu toczącego się bez poślizgu po zewnętrznym obwodzie innego nieruchomego okręgu o tej samej średnicy. Kardioida jest odmianą epicykloidy.
 

Równanie kartezjańskie:  (x² + y² – 2ax)² = 4a²(x² + y²)

Układ współrzędnych biegunowych:  r = 2a (1 + cos())
 

  Kardioida była badana przez Roemera (1674). Nazwy kardioida (sercokształtna; słowo pochodzenia greckiego) użył po raz pierwszy Castillon w Philosophical Transactions of the Royal Society w 1741 roku. Długość tej krzywej wyznaczył La Hire w 1708 roku: długość obwodu kardioidy o parametrze a wynosi 16a, zamknięta nią powierzchnia równa jest 6a². Pole powierzchni obrotowej powstałej z obrotu dokoła osi symetrii łuku kardioidy ma wartość 128a²/5, na tomiast objętość bryły ograniczonej tą powierzchnią wynosi 64a³/3

 

 
KRZYWA ŁAŃCUCHOWA
 

    Krzywa łańcuchowa stanowi kształt idealnie giętkiego, jednorodnego i nierozciągliwego łańcucha, zawieszonego na swoich końcach i przyciąganego grawitacyjnie.
 

 
Równanie kartezjańskie:  
y = a cosh(x/a) = a (e^x/a + e^-x/a)/2;

(wzór na krzywą łańcuchową jest to uogólniony wzór na cosinus hiperboliczny)
 

 Równanie tej krzywej otrzymał Leibniz, Huygens i Johann Bernoulli w 1691 roku.
   W 1669 r. Jungius obalił twierdzenie Galileusza mówiące, iż swobodnie wiszący łańcuch będzie tworzyć parabolę.
   Równanie krzywej łańcuchowej znalazło zastosowanie m.in. przy projektowaniu napowietrznych linii elektroenergetycznych, gdzie opisuje ono zwis przewodów pomiędzy dwoma sąsiednimi słupami

 
OKRĄG
 

 
Równanie kartezjańskie:  x² + y² = a²

Układ równań parametrycznych:  x = a cos(t), y = a sin(t)

Układ współrzędnych biegunowych:  r = a
 

 
   Starożytni Grecy uważali, iż geometrię odkryli Egipcjanie. Skryba Ahmes, autor papirusu Rhind’a, podaje dla wyznaczenia powierzchni okręgu następującą wartość liczby  = 256/81 równe ok. 3,16. Pierwsze twierdzenia związane z okręgiem przypisuje się Talesowi i pochodzą z ok. roku 650 p.n.e. Księga III Elementów Euklidesa omawia właściwości okręgów oraz problemy wpisywania i opisywania wieloboków po okręgu. Apoloniusz wykazał ok. roku 240 p.n.e., iż równanie dwubiegunowe r = kr’ reprezentuje układ współosiowych okręgów wraz ze zmianą wartości k.
 

 
CISSOIDA DIOKLESA
 

 
Równanie kartezjańskie:  y² = x³/(2a – x)
 

 
     Niniejszą krzywę po raz pierwszy zbadał Diokles ok. roku 180 p.n.e. Huygens oraz Wallis odkryli w 1658 roku, iż powierzchnia pomiędzy krzywą a jego asymptotą wynosi  3a².
   Newton opracował metodę rysowania cysoidy Dioklesa przy pomocy dwóch odcinków prostych o jednakowej długości i ułożonych pod odpowiednim kątem do siebie.
   Cysoida pozwoliła Dioklesowi na rozwiązanie problemu podwojenia sześcianu
i w tym właśnie celu została skonstruowana.