|
|
 |
BRYŁY PLATONA
Istnieje pięć brył Platona
Poniżej pokazano 5 brył Platona (lub bryły regularne wielościenne). Dla każdej bryły istnieje siatka do wydrukowana na kartonie. Można wykonać swoje własne bryły Platona, wycinając i sklejając je z kartonu.
Czworościan (tetraedr)
Posiada:
- 4 powierzchnie
- 4 wierzchołki
- 6 krawędzi Siatka czworościanu
|
|
Wartość powierzchni = √3 × (długość krawędzi)²
Objętość = (√2)/12 × (długość krawędzi)³
|
|
 |
 |
Czworościan ma piękną właściwość... wszystkie cztery wierzchołki są położone względem siebie w tej samej jednakowej odległości. I jest to jedyna bryła Platona nieposiadająca równoległych płaszczyzn. Ponadto w czworościanie regularnym wszystkie płaszczyzny są tego samego kształtu i rozmiaru.
Czworościan, który ma 4 jednakowe płaszczyzny, ma równą szansę upadku na dowolną płaszczyznę. | |
|
Zauważmy, że równą szansę upadku na dowolną płaszczyznę mają wszystkie bryły Platona!
Rzetelna kostka do gry
W matematyce rzetelna kostka do gry to taka kostka, która ma jednakową szansę upadku na dowolną swoją powierzchnię.
|
|
 |
 |
Większość z nas myśli o takich kostkach do gry...
…lecz wszystkie bryły Platona mogą służyć jako kostki do gry:
|
|
Używając brył Platona, możemy mieć kostkę z 4, 6, 8, 12 oraz 20 płaszczyznami! Ale przy odrobinie wyobraźni można mieć rzetelną kostkę z dowolną liczbą płaszczyzn.
|
|
Co myślisz o tych interesujących kostkach?
|
 |
Lub o tej z 10 płaszczyznami? |
|
Sześcian (sześciobok)
Siatka sześcianu
|
|
Sześcian ma interesujące właściwości
Posiada:
- 6 płaszczyzn
- 8 wierzchołków, a w każdym wierzchołku spotykają się 3 krawędzie
- 12 krawędzi
- Każda płaszczyzna ma 4 krawędzie i jest kwadratem
Ośmiościan (oktaedr)
Posiada:
- 8 płaszczyzn
- 6 wierzchołków
- 12 krawędzi
Siatka ośmiościanu
|
|
Ośmiościan ma interesujące właściwości:
Posiada:
- 8 płaszczyzn
- Każda płaszczyzna ma 3 krawędzie i jest trójkątem równobocznym
- 12 krawędzi
- 6 wierzchołków i przy każdym wierzchołku spotykają się 4 krawędzie
Wartość powierzchni = 2 × √3 × (długość krawędzi)²
Objętość = (√2)/3 × (długość krawędzi)³
|
|
 |
 |
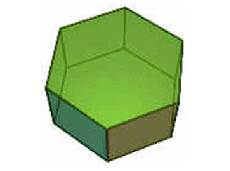
| Gdy mówimy „ośmiościan”, mamy często na myśli „regularny ośmiościan” (wszystkie płaszczyzny są tego samego kształtu i wielkości), ale istnieją ośmiościany nieregularne, jak pokazano obok. Lepiej może nazywać tę bryłę sześciokątnym graniastosłupem lub pryzmatem. | |
|
 |
 |
| 8-boczna kostka? Oczywiście! Ośmiościan ma 8 jednakowych płaszczyzn i równe szanse upadku na dowolną płaszczyznę. | |
|
Dwunastościan
Posiada:
- 8 płaszczyzn. Każda ma 5 krawędzi i stanowi pięciokąt
- 20 wierzchołków. Przy każdym wierzchołku spotykają się 3 krawędzie
- 30 krawędzi
Siatka dwunastościanu
|
|
Wielkość powierzchni = 3×√(25+10×√5) × (długość krawędzi)²
Objętość = (15+7×√5)/4 × (długość krawędzi)³
|
|
 |
 |
|
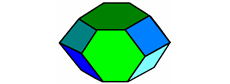
Gdy mówimy „dwunastościan”, mamy często na myśli „regularny dwunastościan” (wszystkie płaszczyzny są tego samego kształtu i wielkości), ale istnieją dwunastościany nieregularne, jak pokazano obok. | |
|
 |
 |
| 12-ścienna kostka? Oczywiście! Dwunastościan, który ma 12 jednakowych płaszczyzn ma przy rzucie równe szanse upadku na dowolną płaszczyznę | |
|
Dwudziestościan
Posiada:
- 20 płaszczyzn. Każda płaszczyzna ma 3 krawędzie
i stanowi trójkąt równoboczny
- 12 wierzchołków
- 30 krawędzi
Siatka dwudziestościanu
|
|
Wartość powierzchni = 5×√3 × (długość krawędzi)²
Objętość = 5×(3+√5)/12 × (długość krawędzi)³
|
|
 |
 |
|
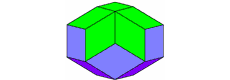
Gdy mówimy „dwudziestościan”, mamy często na myśli „regularny dwudziestościan” (wszystkie płaszczyzny są tego samego kształtu i wielkości), ale istnieją dwudziestościany nieregularne, jak pokazano obok. | |
|
 |
 |
|
20-boczna kostka? Oczywiście! Dwudziestościan ma 20 jednakowych płaszczyzn i jednakowe szanse upadku na dowolną płaszczyznę przy rzucie. | |
|
|
 |
|

