|
|
 |
Raport z II edycji
Ogólnopolskiej Olimpiady Logiczno-Matematycznej
w roku szkolnym 2011 - 2012
|
|
„Matematyka wyposaża nas w coś, jakby nowy zmysł”
Charles Robert Darwin
|
|
Administracja portalu Zadane.pl, biorąc pod uwagę ogromne zainteresowanie uczniów ze wszystkich poziomów edukacji oraz pozytywne opinie dotyczące organizacji i przebiegu I edycji Ogólnopolskiej Olimpiady Logiczno - Matematycznej postanowiła w roku szkolnym 2011-2012 zorganizować kolejną edycję tego konkursu.
Innowacyjna formuła pozwalająca wszystkim chętnym uczniom na sprawdzenie swojej wiedzy matematycznej poprzez Internet, zyskała również aprobatę Ministra Edukacji Narodowej, który w lipcu 2011 r. przyznał Olimpiadzie honorowy patronat.
Wraz z początkiem roku szkolnego rozpoczął się nabór do kolejnej edycji Olimpiady. Od 5 września 2011 r. uczniowie zainteresowani udziałem w konkursie, chcąc wziąć w nim udział, musieli zarejestrować się na stronie Olimpiady, gdzie mogli rozwiązywać zestawy przygotowawcze. Na wszystkich trzech poziomach przykładowe zestawy konkursowe rozwiązało 18421 osób.
Podobnie jak w poprzedniej edycji, wszystkie zadania zostały przygotowane przez zespół nauczycieli matematyki, którzy na stałe współpracują z portalem Zadane.pl oraz posiadają uprawnienia egzaminatorów OKE. Ponadto, w tej edycji Olimpiady został powołany Zespół Merytoryczny w składzie: dr Arkadiusz Lisak (wieloletni pracownik naukowo-dydaktyczny Wyższej Szkoły Informatyki i Zarządzania w Rzeszowie, obecnie w Wyższej Szkole Inżynieryjno-Ekonomicznej w Rzeszowie, były kierownik Zespołu Analitycznego WSIiZ, autor podręcznika z matematyki dla studentów) i mgr Piotr Drąg (nauczyciel akademicki Wyższej Szkoły Informatyki i Zarządzania, asystent w Katedrze Matematyki i Podstaw Informatyki, nauczyciel dydaktyczny w Liceum Ogólnokształcącym w Boguchwale), który nadzorował pracę zespołu zadaniowego w zakresie poprawności zadań i odpowiedzi.
W pierwszym etapie olimpiady trwającym od 3 października do 13 listopada 2011 r. łącznie na trzech poziomach wzięło 9236 osób, z czego wynik dodatni za test o „łatwym” stopniu trudności uzyskało 8977 osób, za test o „średnim” stopniu trudności uzyskało 5493 osób, a za test „trudny” 3129 osób.
Zestaw „łatwy” obejmował zadania wprowadzające i zachęcające do intelektualnego wysiłku oraz rozszerzania wiedzy i zainteresowań matematycznych, natomiast zestaw „średni’ i „trudny” zawierał zadania do rozwiązania, których wymagany zakres i poziom wiedzy jest wystarczający do uzyskania odpowiednio oceny bardzo dobrej lub celującej na zakończenie nauki matematyki na danym poziomie edukacyjnym.
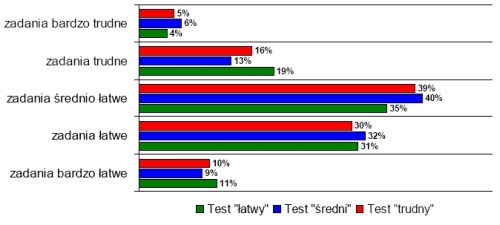
W tegorocznej edycji Olimpiady wzięło udział 3078 uczniów szkół podstawowych. Analiza wyników pierwszego etapu olimpiady wykazała, że zadania dla uczestników na poziomie podstawowym były średnio łatwe. Na wykresie 1 przedstawiono procentowy rozkład ilości zadań ze względu na wskaźnik łatwości zadań w poszczególnych testach. Najtrudniejszymi zadaniami dla uczniów szkół podstawowych były zadania dotyczące przekształcania wyrażeń algebraicznych oraz zadania z geometrii, zarówno dotyczące figur płaskich, jak i figur przestrzennych, a najłatwiejsze okazały się zadania ze statystyki.
Pozytywny wynik z testu o łatwym stopniu trudności uzyskało 2992 uczestników poziomu podstawowego, w tym 39 osób uzyskało maksymalną ilość punktów, a z testu o średnim poziomie trudności 1831 uczestników, w tym maksymalną ilość punktów uzyskały 33 osoby. Test trudny pozytywnie zaliczyło 1038 uczestników, w tym 19 osób uzyskało maksymalną ilość punktów. Natomiast ze wszystkich trzech testów w I etapie olimpiady na poziomie podstawowym maksymalną ilość punktów uzyskały cztery osoby. Do finału olimpiady jury zakwalifikowało 56 uczniów, co stanowi 1,82% wszystkich uczestników I etapu na poziomie podstawowym.
|
|
Wykres 1. Rozkład ilości zadań ze względu na wskaźnik łatwości zadań w poszczególnych testach Poziom podstawowy
|
|
 |
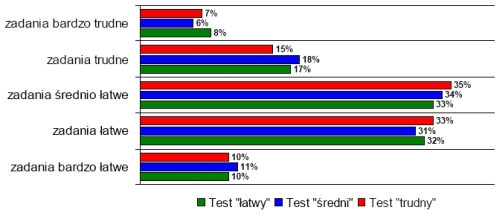
W Olimpiadzie uczestniczyło 3021 gimnazjalistów, dla których zadania we wszystkich trzech stopniach trudności były, podobnie jak dla uczniów szkół podstawowych, średnio łatwe (wykres 2). Najłatwiejszymi zadaniami dla gimnazjalistów w I etapie olimpiady były zadania z algebry oraz zadania dotyczące figur płaskich, znacznie trudniejsze okazały się zadania z funkcji.
Pozytywny wynik z testu o łatwym stopniu trudności uzyskało 2873 gimnazjalistów, w tym 35 osób uzyskało maksymalną ilość punktów, a z testu o średnim poziomie trudności 1758, w tym maksymalną ilość punktów uzyskało 15 osób. Test trudny pozytywnie zaliczyło 1024 uczestników, w tym 7 osób uzyskało maksymalną ilość punktów. Natomiast ze wszystkich trzech testów w I etapie Olimpiady na poziomie gimnazjalnym, tylko dwie osoby uzyskały maksymalną ilość punktów. Do finału Olimpiady jury zakwalifikowało 53 uczniów, co stanowi 1,75% wszystkich uczestników I etapu na poziomie gimnazjalnym.
|
|
Wykres 2. Rozkład ilości zadań ze względu na wskaźnik łatwości zadań w poszczególnych testach Poziom gimnazjalny
|
|
 |
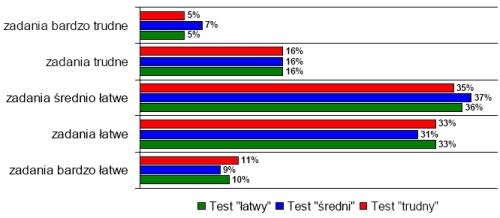
W II edycji Olimpiady wzięło udział 3137 uczniów szkół ponadgimnazjalnych. Analiza łatwości zadań w poszczególnych testach wykazała, że zadania, bez względu na stopień trudności testu, również dla uczniów szkół średnich były średnio łatwe, co przedstawiono na wykresie 3. Najłatwiejsze na tym poziomie Olimpiady okazały się dla uczestników zadania z trygonometrii i ciągów, natomiast najtrudniejszymi zadaniami były dla nich zadania z geometrii analitycznej i stereometrii.
Z testu o łatwym stopniu trudności pozytywny wynik uzyskało 3112 uczniów szkół średnich, w tym 58 osób uzyskało maksymalną ilość punktów, a z testu o średnim poziomie trudności 1904, w tym maksymalną ilość punktów uzyskały 24 osoby. Test trudny pozytywnie zaliczyło 1067 uczestników, w tym 16 osób uzyskało maksymalną ilość punktów. Jednak ze wszystkich trzech testów w I etapie Olimpiady na poziomie ponadgimnazjalnym, tylko dwie osoby uzyskała maksymalną ilość punktów. Do finału Olimpiady jury zakwalifikowało 61 uczniów, co stanowi 1,94% wszystkich uczestników I etapu na poziomie ponadgimnazjalnym.
|
|
Wykres 3. Rozkład ilości zadań ze względu na wskaźnik łatwości zadań w poszczególnych testach Poziom ponadgimnazjalny
|
|
 |
W pierwszym etapie Olimpiady każdy zestaw zawierał 20 zdań testowych jednokrotnego wyboru, który w zależności od stopnia trudności należało rozwiązać odpowiednio w czasie 120, 150 lub 180 minut. Natomiast uczestnicy finału, który odbył się 6 marca 2012 r., na wszystkich poziomach Olimpiady, rozwiązywali zestaw 15 zadań składający się z 10 zdań testowych oraz 5 zdań otwartych z zakresu programu olimpiady, ze szczególnym uwzględnieniem zadań sprawdzających umiejętności operowania zdobytą wiedzą w rozwiązywaniu zadań nietypowych i zadań o podwyższonym stopniu trudności oraz zadań problemowych. Na rozwiązanie zadań uczestnicy finału mieli 120 minut.
Tegoroczny finał Olimpiady odbył się w szkolnych pracowniach komputerowych w warunkach kontrolowanej samodzielności, czyli pod nadzorem nauczyciela prowadzącego wskazanego przez dyrektora szkoły macierzystej finalisty. W tym miejscu należą się słowa uznania zarówno dyrektorom szkół, jak i opiekunom, za sprawną organizację finału Olimpiady w swoich placówkach.
W opinii uczestników Olimpiady i ich opiekunów zmiana formuły organizacji finału, przyniosła nie tylko duże zainteresowanie samym konkursem, lecz wpłynęła również na zwiększenie liczby uczestników, ponieważ umożliwia uczestnictwo w niej wszystkim chętnym, bo to uczeń sam decyduje, czy chce sprawdzić swoją wiedzę i umiejętności poprzez rozwiązywanie zadań konkursowych pierwszego etapu. Ponadto, przeprowadzanie Olimpiady przez Internet pozwala nie tylko zaoszczędzić koszty podróży, ale daje także szansę wszystkim uczniom, którzy lubią matematykę, a przede uczniom z małych miejscowości, w sprawdzeniu swoich możliwości w sytuacjach wymagających rywalizacji. Jednocześnie pokazuje uczniom, że nauka może być ciekawa, a Internet to doskonałe medium umożliwiające poszerzanie swojej wiedzy i wiadomości.
Do finału Olimpiady jury zakwalifikowało ogółem 170 uczniów. Zadnia finałowe rozwiązało i przesłało do oceny 165 uczniów, trzech uczniów nie przystąpiło do finału oraz dwóch uczniów zostało zdyskwalifikowanych za nieprzestrzeganie Regulaminu Olimpiady.
Analiza rozwiązań zadań finałowych wykazała, że najlepiej w tegorocznej edycji Olimpiady wypadli uczniowie szkół ponadgimnazjalnych – średnia liczba punktów za cały zestaw finałowy wyniosła 41 pkt., a najgorzej uczniowie gimnazjów – uzyskując za cały zestaw finałowy średnio 36 pkt., ale jednocześnie tylko uczeń gimnazjum za rozwiązanie całego zestawu finałowego uzyskał maksymalną liczbę punktów, czego nie udało się osiągnąć żadnemu uczestnikowi finału na poziomie podstawowym i ponadgimnazjalnym.
Biorąc pod uwagę wyniki z poszczególnych poziomów Olimpiady za rozwiązanie zadań zamkniętych, najlepiej z tą częścią zestawu zadań finałowych poradzili sobie uczniowie gimnazjum - ośmioro finalistów z tej części otrzymało maksymalną liczbę punktów, a najgorzej wypadli uczniowie szkół podstawowych, bo tylko czterech uczestników finału rozwiązało tę cześć bezbłędnie. Zdecydowanie gorzej finaliści radzili sobie z zadaniami otwartymi, bo tylko uczeń gimnazjum bezbłędnie rozwiązał tę cześć zestawu finałowego. W tym miejscu szczególne podziękowania należy złożyć autorom zadań i zespołowi merytorycznemu za ich pomysłowość w pracy nad zadaniami oraz za przygotowanie wzorcowych rozwiązań. Biorą oni na siebie dużą odpowiedzialność, ponieważ to ich rozwiązania są bezpośrednio konfrontowane z rozwiązaniami uczestników.
Szczegółowa analiza wszystkich rozwiązań zadań otwartych z poszczególnych zestawów finałowych wykazała, że im trudniejsze zadanie, tym większy był stosunek liczby sposobów rozwiązań do liczby poprawnych rozwiązań, natomiast w zadaniach o niskim współczynniku trudności liczba sposobów rozwiązań była mała, gdyż dało się w nich dostrzec prostą drogę prowadzącą do rozwiązania. Ponadto, w zadaniach trudnych uczniowie nie zawsze widzieli jasno drogę rozwiązania i dość często błądzili po omacku.
W tegorocznej edycji Olimpiady uczniom szkół podstawowych największą trudność sprawiło zadanie zamknięte, w którym należało wykazać się wiedzą dotyczącą własności działań na liczbach oraz zadanie zawierające obliczenia miar kątów. Z kolei dla gimnazjalistów najtrudniejszym zadaniem zamkniętym okazało się zadanie z wykorzystaniem warunku prostopadłości prostych oraz zadanie z planimetrii dot. kątów wewnętrznych wielokąta foremnego. Natomiast dla uczniów szkół średnich najtrudniejszym zadaniem zamkniętym było zadanie z trygonometrii oraz zadanie z wykorzystaniem własności funkcji wykładniczej.
Spośród zadań otwartych najtrudniejszym zadaniem dla uczniów szkół podstawowych było zadanie z uwzględnieniem dodawania i odejmowania prędkości nurtu rzeki, dla gimnazjalistów najtrudniejszym zadaniem okazało zadanie polegające na wykorzystaniu jednoznaczności rozkładu liczby całkowitej na czynniki pierwsze. Natomiast dla uczniów szkół ponadgimnazjalnych najtrudniejszym zadaniem było zadanie, w którym należało wykorzystać własność funkcji parzystej.
Biorąc pod uwagę zarówno rozwiązania z I etapu konkursu, jak i rozwiązania finałowe, możemy stwierdzić, że uczestnicy tegorocznej edycji olimpiady szczególnie dobrze potrafią: |
|
- stosować znane algorytmy,
- rozwiązywać zadania optymalizacyjne i kombinatoryczne,
- rozwiązywać zadania w kilku prostych krokach,
- odczytywać i przetwarzać informacje przedstawione na rysunku.
Natomiast mieli pewne trudności: |
|
- z podaniem kompletnego rozwiązania niestandardowego zadania,
- z myśleniem abstrakcyjnym, które wymagało analizy lub uogólnienia,
- w stosowaniu technik twórczego myślenia do rozwiązania zadania problemowego, łączącego wiedzę z zakresu fizyki i matematyki,
- z interpretowaniem własności funkcji,
- z wykorzystaniem własności figur.
Analiza wyników oraz opinie jej uczestników i ich opiekunów, pozwalają nam stwierdzić, że Olimpiada osiągnęła postawione cele: |
|
- rozwijanie zamiłowania do matematyki,
- promowanie zdolności matematycznych,
- odkrywanie talentów matematycznych,
- doskonalenie umiejętności rozwiązywania zadań i problemów matematycznych,
- wdrażanie do stosowania i wykorzystania komputera w edukacji,
- kształtowanie umiejętności zdobywania wiedzy,
- pobudzanie aktywności poznawczej.
Jednak zadajemy sobie sprawę, że aby wymienione wyżej cele były nadal realizowane, to administracja portalu Zadane.pl, czyli organizator Ogólnopolskiej Olimpiady Logiczno – Matematycznej, wspólnie z opiekunami uczestników kolejnych edycji konkursu, powinni dołożyć wszelkich starań, by każdy uczeń miał szanse wzięcia w niej udziału, bo zgadzamy się ze słowami Stanisława Wielgusa, który uważa, że „…matematyka gimnastykuje umysł ucznia, w sposób niedostrzegalny, czyni go elastycznym, tak by mógł sobie dawać radę w najbardziej nieoczekiwanych intelektualnie sytuacjach, by był twórczy i samodzielny”. Ponadto, potrzebna jest mentalna zmiana w podejściu nauczycieli do sposobu kształcenia uczniów utalentowanych matematycznie. Należy, bowiem pamiętać o słowach Georg Christopha Lichtenberga, że „…to, co musiałeś odkryć samodzielnie zostawia w twym umyśle ścieżkę, którą w razie potrzeby możesz pójść jeszcze raz”. Dlatego główny nacisk nie powinien być kładziony na uczenie stosowania typowych metod rozwiązań, gdyż to prowadzi do prób sprowadzania rozwiązywania zadań do odtwórczego i automatycznego stosowania tychże metod i algorytmizacji procesu rozwiązywania zadań konkursowych, ale należy skupić się na kształceniu umiejętności stosowania strategii ogólnych, a w dalszej kolejności strategii szczegółowych.
Przedstawione wyżej zalecenia z pewnością już realizują i nadal będą realizowali opiekunowie tegorocznych laureatów Ogólnopolskiej Olimpiady Logiczno – Matematycznej przedstawionych w tabeli 1. W tym miejscu gratulujemy wszystkim laureatom sukcesu w rywalizacji o laury olimpijskie oraz życzymy wielu korzyści płynących ze zgłębiania wiedzy matematycznej, a także powodzenia i wielu radości w odkrywaniu świata matematyki.
Oczywiście nie wszyscy uczestnicy Olimpiady mogą zostać jej laureatami - na podium jest bowiem tylko 8 miejsc dla najlepszych jej uczestników. Niemniej wszyscy uczestnicy Olimpiady wygrywają przez sam fakt wzięcia w nich udziału. Poświęcają bowiem czas i energię na zgłębianie wiedzy matematycznej niezbędnej do codziennego życia we współczesnym świecie. Mamy również nadzieję, że parafrazując słowa Arystotelesa wszyscy uczestnicy olimpiady „słodko spożywają matematykę …, a skosztowawszy jej, nie będą chcieli już od niej odstąpić…”.
|
|
Tab. 1 Wykaz laureatów II edycji Ogólnopolskiej Olimpiady Logiczno – Matematycznej
|
|
Duże zainteresowanie możliwością sprawdzenia swojej wiedzy matematycznej napawa organizatorów Olimpiady optymizmem, ponieważ te liczby świadczą o tym, iż uczniowie zdają sobie sprawę z tego, że życie bez matematyki jest nierealne. Każdy z nich wie, że matematyka opisuje różne zależności, z którymi spotykają się w codziennym życiu: przeliczają zakupy, obliczają procentowe obniżki w sklepach, liczą ile metrów kwadratowych ma łazienka, aby móc kupić odpowiednią liczbę glazury czy terakoty. Zastanawiają się nad tym, ile należy skreślić zakładów w Lotto, aby przybliżyć się do głównej wygranej, i nad tym, czy dałoby się obliczyć wysokość drzewa bez wchodzenia na nie. Biorący udział w Olimpiadzie uczniowie wiedzą, że na te i na wiele innych pytań odpowiedź ma matematyka. |
|
|
 |
|

