|
|
 |
Raport z I edycji
Ogólnopolskiej Olimpiady Logiczno-Matematycznej
zorganizowanej w roku szkolnym 2010-2011 |
|
Ogólnopolska Olimpiada Logiczno-Matematyczna została zorganizowana w celu rozwijania zamiłowania do matematyki, promowania zdolności matematycznych, kształtowania umiejętności zdobywania wiedzy oraz pobudzenia aktywności poznawczej uczniów.
Pamiętając słowa Georga Polya, że „zadanie matematyczne może być taką rozrywką, jak krzyżówka i może tak smakować, jak ciastko z malinami”, administracja portalu zadane.pl (organizatora i pomysłodawcy Olimpiady) dała szansę wszystkim uczniom, którzy kochają matematykę, jak i tym, którzy zechcieli się sprawdzić i nauczyć czegoś nowego w zasmakowaniu rywalizacji, doświadczeniu wspaniałych emocji oraz znakomitej zabawie, jaką jest możliwość rozwiązywania zadań konkursowych. Jednocześnie organizatorzy olimpiady pokazali, że nauka może być ciekawa, a Internet może stać się doskonałym narzędziem do promowania aktywności intelektualnej, samorozwoju, poszerzania wiedzy oraz samej edukacji i nauki.
Ogólnopolska Olimpiada Logiczno-Matematyczna jest skierowana do uczniów szkół podstawowych, gimnazjalnych oraz ponadgimnazjalnych.
Olimpiada rozpoczęła się 4 października br., ale już od 1 września na stronie olimpiady: http://olimpiadamatematyczna.pl/, uczniowie mogli przećwiczyć rozwiązywanie zadań oraz zapoznać się ze sposobem udzielania odpowiedzi – w tym celu stworzono przykładowe zestawy zadań dla poszczególnych poziomów edukacyjnych.
Program merytoryczny olimpiady został oparty na wymaganym zakresie i poziomie wiedzy na zakończenie nauki poszczególnych poziomów edukacyjnych.
Organizator olimpiady, biorąc pod uwagę słowa Alexandra Wesmana: „Pisanie zadań jest z natury twórcze – jest sztuką. Tak, jak nie może być przepisu na produkcję dobrego obrazu lub dobrej powieści, tak nie może być reguł, które dadzą gwarancję skonstruowania dobrego zdania testowego”, do opracowania zadań przygotowawczych i konkursowych powołał zespół składający się z nauczycieli matematyki, którzy na stałe współpracują z portalem oraz posiadają uprawnienia egzaminatorów OKE. Zespół opracował w sumie tysiąc zadań testowych dla poszczególnych poziomów olimpiady, o różnym stopniu trudności. Opracowane zadania obejmują wszystkie działy zawarte w zakresie obowiązujących treści olimpiady, który stanowi załącznik do regulaminu.
Dla każdego poziomu olimpiady, który pokrywa się z poziomami edukacyjnym zaplanowano dwa etapy olimpiady.
Pierwszy etap trwający od 4 października do 28 listopada br., polegał na rozwiązywaniu zadań testowych na stronie internetowej olimpiady. Na tym etapie uczestnicy rozwiązywali trzy różniące się stopniem trudności zestawy zadań, które ukazywały się w określonym w regulaminie terminie. Każdy zestaw, który w zależności od stopnia trudności należało rozwiązać odpowiednio w czasie 120, 150 lub 180 minut, zawierał 20 zdań testowych jednokrotnego wyboru. Zestaw pierwszy „łatwy” obejmował zadania wprowadzające i zachęcające do intelektualnego wysiłku oraz rozszerzania wiedzy i zainteresowań matematycznych, zestaw drugi „średni’ i trzeci „trudny” zawierał zadania do rozwiązania, których wymagany zakres i poziom wiedzy jest wystarczający do uzyskania odpowiednio oceny bardzo dobrej lub celującej na zakończenie nauki matematyki na danym poziomie edukacyjnym. W każdym zestawie zadań za udzielenie dobrej odpowiedzi do zadania uczestnik olimpiady otrzymywał + 5 punktów, za udzielenie złej odpowiedzi do zadania – 2 punkty, a za brak odpowiedzi do zadania – 1 punkt.
Próbne – przygotowawcze zestawy zadań łącznie na wszystkich trzech poziomach rozwiązało 11118 osób, w tym 6922 dziewcząt i 4196 chłopców. Zadania konkursowe w pierwszym internetowym etapie olimpiady łącznie na trzech poziomach rozwiązało 8768 osób, z czego wynik dodatni za test o „łatwym” stopniu trudności uzyskało 8277 osób, za test o „średnim” stopniu trudności uzyskało 5281 osób, a za test „trudny” 2936 osób.
Analiza testów przygotowawczych wykazała, że zadania na poziomie podstawowym były średnio łatwe (wskaźnik łatwości testu wyniósł 0,51) – maksymalny wynik z testu uzyskały 92 osoby, na poziomie gimnazjalnym zadania okazały się trudne (wskaźnik łatwości testu wyniósł 0,35) – maksymalny wynik z testy uzyskało 133 osób, na poziomie ponadgimnazjalnym zadania były średnio łatwe (wskaźnik łatwości testu wyniósł 0,47) – maksymalny wynik uzyskało 116 osób. Wszystkie testy przygotowawcze były umiarkowanie rzetelne, współczynnik rzetelności testów obliczony wzorem KR20 i metodą połówkową mieścił się w przedziale +0,81 do +0,90.
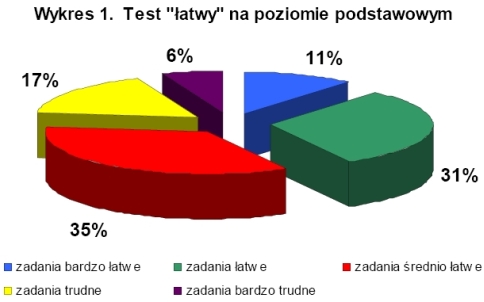
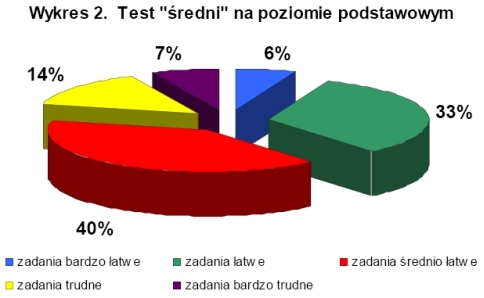
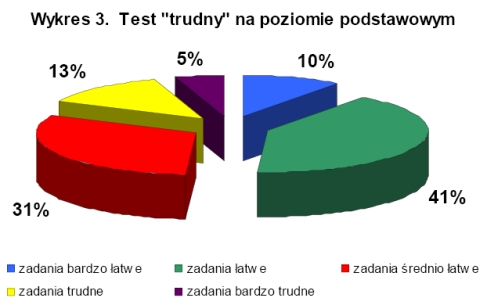
Badanie wyników na poziomie podstawowym wykazało, że zadania, bez względu na stopień trudności testu, były dla uczestników olimpiady średnio łatwe, a testy były o wysokiej rzetelności (współczynnik rzetelności testów obliczony wzorem KR20 i metodą połówkową mieścił się w przedziale +0,91 do +1,00). Na wykresach 1-3 przedstawiono procentowy rozkład ilości zadań ze względu na wskaźnik łatwości w poszczególnych testach Najtrudniejszymi zadaniami dla uczestników olimpiady na poziomie podstawowym były zadania dotyczące figur przestrzennych, a najłatwiejsze okazały się zadania ze statystyki.
W olimpiadzie na poziomie podstawowym udział wzięło 2028 osób, maksymalną ilość punktów za test o łatwy stopniu trudności uzyskało 7 osób, o średnim stopniu trudności 6 osób, a o trudnym trzy osoby. W pierwszym etapie olimpiady na poziomie podstawowym ze wszystkich trzech testów tylko jedna osoba uzyskała maksymalną ilość punktów. Jury olimpiady do drugiego etapu zakwalifikowało 50 osób, co stanowi 2,5% wszystkich uczestników pierwszego etapu na poziomie podstawowym. |
|
 |
 |
 |
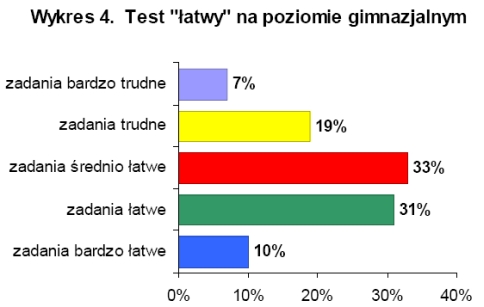
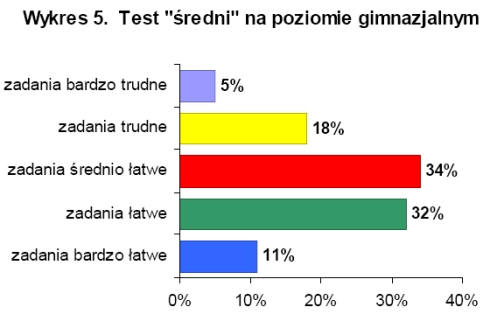
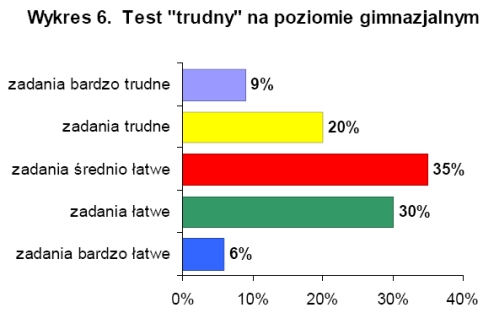
Na poziomie gimnazjalnym analiza wyników testów wykazała, że zadania z testów o łatwym i średnim stopniu trudności były dla uczestników olimpiady średnio łatwe, a zadania z testu o trudnym stopień trudności okazały się dla uczestników olimpiady zadaniami trudnymi. Testy o łatwym i trudnym stopniu trudności były testami o wysokiej rzetelności. Na wykresach 4-6 przedstawiono procentowy rozkład ilości zadań ze względu na wskaźnik łatwości w poszczególnych '74estach Najłatwiejszymi zadaniami dla uczestników olimpiady na poziomie gimnazjalnym były zadania dotyczące figur płaskich, a najtrudniejsze okazały się zadania z algebry.
W olimpiadzie na poziomie gimnazjalnym udział wzięło 3882 osób, maksymalną ilość punktów za test o łatwy stopniu trudności uzyskały 22 osoby, o średnim stopniu trudności 9 osób, a o trudnym dwie osoby. W pierwszym etapie olimpiady na poziomie podstawowym ze wszystkich trzech testów tylko jedna osoba uzyskała maksymalną ilość punktów. Jury olimpiady do drugiego etapu zakwalifikowało 50 osób, co stanowi 1,3% wszystkich uczestników pierwszego etapu na poziomie gimnazjalnym. |
|
 |
 |
 |
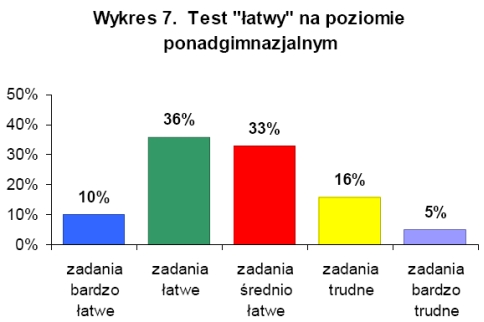
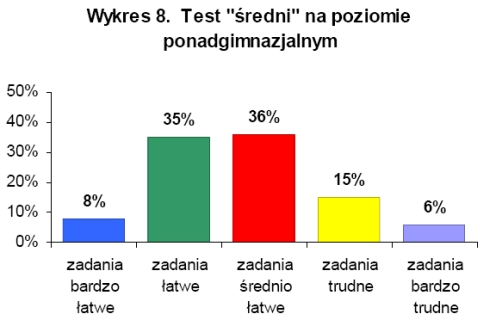
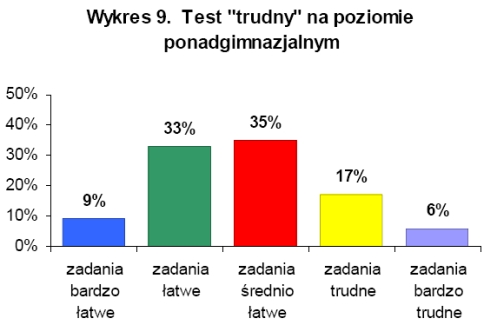
Analizując wyniki testów na poziomie ponadgimnazjalnym ustalono, że zadania, bez względu na stopień trudności testu, były dla uczestników olimpiady średnio łatwe, a wszystkie testy były o wysokiej rzetelności. Na wykresach 7-9 przedstawiono procentowy rozkład ilości zadań ze względu na wskaźnik łatwości w poszczególnych testach Najtrudniejszymi zadaniami dla uczestników olimpiady na poziomie ponadgimnazjalnym były zadania z geometrii analitycznej, a najłatwiejsze okazały się z trygonometrii i ciągów.
W olimpiadzie na poziomie ponadgimnazjalnym udział wzięło 2858 osób, maksymalną ilość punktów za test o łatwy stopniu trudności uzyskało 13 osób, o średnim stopniu trudności 4 osoby, a o trudnym jedna osoba. W pierwszym etapie olimpiady na poziomie ponadgimnazjalnym ze wszystkich trzech testów żadna osoba nie uzyskała 1,7% wszystkich uczestników pierwszego etapu na poziomie ponadgimnazjalnym. |
|
 |
 |
 |
Drugi etap olimpiady - Finał odbył się 26 marca 2011 r. W finale wszystkich poziomów olimpiady finaliści rozwiązywali zestaw 15 zadań składający się z 10 zdań testowych oraz 5 zdań otwartych z zakresu programu olimpiady, ze szczególnym uwzględnieniem zadań sprawdzających umiejętności operowania zdobytą wiedzą w rozwiązywaniu zadań nietypowych i zadań o podwyższonym stopniu trudności oraz zadań problemowych. Czas na rozwiązanie zadań z zestawu finałowego wynosił 120 min.
Analizując wyniki finału Ogólnopolskiej Olimpiady Logiczno-Matematycznej możemy stwierdzić, że wielu jej uczestników, mimo że zna procedurę rozwiązywania zadań, w momencie ustalenia rozwiązania, zapominało o sprawdzeniu poprawności rozwiązania. Jednak ogólne wyniki olimpiady skłaniają do refleksji, że mamy sporą rzeszę uczniów nie tylko „nauczonych”, ale potrafiących z przekazanej im wiedzy korzystać.
Finałowy zestaw zadań, dla każdego poziomu olimpiady, składał się z dziesięciu zadań zamkniętych oraz z pięciu zadań otwartych. Ze względu na specyficzną formułę konkursu – uczestnicy, na każdym jej etapie rozwiązywali zestawy zadań przez Internet – zadania otwarte w zestawie finałowym nie mogły zawierać zadań, których zapis rozwiązania byłby skomplikowany oraz wymagałby stosowania specjalnego oprogramowania lub dodatkowego sprzętu komputerowego.
Dokonując analizy całego zestawu zadań finałowych, najlepiej wypadli uczniowie szkół podstawowych – średnia liczba punktów za cały zestaw finałowy wyniosła 44 pkt. – niestety żaden uczestnik nie uzyskał maksymalnej liczby punktów. Najgorzej wypadli uczniowie szkół ponadgimnazjalnych i również nikt z uczestników, podobnie jak na poziomie gimnazjalnym, nie uzyskał maksymalnej liczby punktów.
Biorąc pod uwagę wyniki z poszczególnych poziomów olimpiady za rozwiązanie zadań zamkniętych, możemy stwierdzić, że najlepiej z tą częścią zestawu zadań finałowych poradzili sobie uczniowie gimnazjum - sześcioro finalistów z tej części otrzymało maksymalną liczbę punktów, a najgorzej wypadli uczniowie szkół ponadgimnazjalnych, bo tylko dwóch uczestników finału rozwiązało tę cześć bezbłędnie.
Analiza trudności zadań zamkniętych, która została przeprowadzona w oparciu o skalę trudności podaną przez B. Niemierko w książce „Pomiar wyników kształcenia” oraz przyjmując, że „współczynnik trudności” jest stosunkiem liczby uczestników, którzy nie rozwiązali zadania do liczby uczestników biorących udział w finale olimpiady, wykazała, że dla uczniów szkół podstawowych największą trudność sprawiło zadanie z wartością bezwzględną oraz zadanie zawierające obliczenia procentowe, w którym, na co wskazują uzyskane wyniki, to prawdopodobnie nie obliczenia procentowymi stanowiło problem, ale błędna interpretacja pytania. Z kolei dla gimnazjalistów najtrudniejszym zadaniem zamkniętym okazało się zadanie z planimetrii dot. kątów wewnętrznych wielokąta foremnego. Natomiast dla uczniów szkół średnich najtrudniejszym zadaniem zamkniętym było zadanie ze stereometrii dot. kątów trójściennych sześcianu. Uczestnicy finału olimpiady zdecydowanie najlepiej poradzili sobie z zadaniami logicznymi.
Ocena rozwiązania każdego zadania otwartego była wynikiem porozumienia pomiędzy dwoma niezależnie sprawdzającymi dane zadanie członkami jury. Taka procedura oceniania zdaniem organizatorów olimpiady zminimalizowała możliwość popełnienia pomyłek.
Żaden uczestnik olimpiady z części zawierającej zadania otwarte nie uzyskał maksymalnej liczby punktów, najlepiej z zadaniami otwartymi poradzili sobie uczniowie szkół podstawowych, jednak średnia liczba punktów za tę część zestawu zadań stanowiła tylko 38% możliwej do uzyskania maksymalnej liczby punktów.
Współczynnik trudności wszystkich zadań otwartych, na wszystkich poziomach olimpiady, był większy od 0, 4, co w skali trudności zadań oznacza, że zadania otwarte były, co najmniej umiarkowane trudne. Najtrudniejszym zadaniem otwartym dla szkół podstawowych było zadanie logiczne, polegające na stwierdzeniu zależności pomiędzy wartościami wyrażonymi ułamkami, dla gimnazjalistów najtrudniejszym zadaniem okazało zadanie z pozornym rozwiązaniem, które nie spełniało warunków zadania oraz zadanie z planimetrii polegające na zbadaniu istnienia rozwiązania. Natomiast dla uczniów szkół ponadgimnazjalnych najtrudniejszym zadaniem okazało się zadanie polegające na wykorzystaniu związków pomiędzy funkcjami trygonometrycznymi.
Szczegółowa analiza wszystkich rozwiązań zadań otwartych z poszczególnych zestawów finałowych wykazała, że uczestnicy olimpiady popełniali następujące błędy:
• błędy przypadkowe, czyli pomyłki rachunkowe w obliczeniach - zmiana znaku, błędne wykonanie działania na liczbach czy wyrażeniach algebraicznych ,
• błędy logiczne, czyli błędy, które wynikały z niezrozumienia roli założenia i tezy oraz związku miedzy nimi,
• błędy powierzchownej wiedzy, czyli błędy wynikające z braku dostatecznej znajomości twierdzeń i metod matematycznych,
• błędy nieświadome, które uczestnicy popełniali próbując stosować twierdzenia i metody, które im wydały się poprawne,
• błędny wybór metody, który prawdopodobnie wynika z braku dostatecznej wiedzy matematycznej.
Analizując statystyki oraz patrząc na wynik ankiety przeprowadzonej wśród uczestników olimpiady i ich naukowych opiekunów, możemy śmiało stwierdzić, że Olimpiada osiągnęła swój zamierzony cel.
Podsumowując, jako organizator olimpiady chcieliśmy wyjść naprzeciw oczekiwaniom użytkowników jednego z największych polskich portali edukacyjnych - portalu Zadane.pl, a także pomóc wszystkim nieśmiałym, ale zdolnym uczniom naszych polskich szkół, i dlatego postanowiliśmy zorganizować coś, co wielu określało, jako rzecz niemożliwą, czyli przeprowadzić przez Internet - ogólnopolską olimpiadę matematyczną.
Stawiając sobie za cel rozwijanie zamiłowania do „Królowej Nauk” dołożyliśmy wszelkich starań, aby wskazać kierunek, w jakim powinna iść edukacja w Polsce. Jako, że w Polsce już 90% polskich uczniów posiada w swoich domach komputery, chcieliśmy pokazać, że to urządzenie wraz z łączem Internetowym powinno wyznaczać trendy obecnej edukacji.
Coraz więcej słyszy się o e-learningu, nie mniej jednak jest on, jak na razie popularny tylko na niektórych uczelniach wyższych. W szkołach podstawowych, gimnazjach oraz szkołach ponadgimnazjalnych jest to jeszcze mało popularna metoda edukacji. Wszyscy jednak zdają sobie sprawę, że Internet jest medium pokonującym wszelkie granice i ograniczenia czasoprzestrzenne. Pozwala zaoszczędzić nam koszty podróży, daje prawie nieograniczony dostęp do informacji, a także pozwala elastycznie wykorzystywać czas poświęcony na naukę. Ucząc się w domu poprawiamy komfort pracy, nie jesteśmy uzależnieni od narzucanych form edukacji.
Wykonaliśmy pewien krok w edukacji młodzieży, a osobom które niedowierzały, że niemożliwe może stać się możliwe, udowodniliśmy, że Olimpiada może być wspaniałym połączeniem przyjemnego z pożytecznym. Podstawową czynnością na lekcjach matematyki we wszystkich typach szkół jest rozwiązywanie zadań. Każdy uczeń musi nauczyć się sposobów i metod rozwiązywania zadań, które są sprawdzane w czasie sprawdzianów, kartkówek, egzaminów oraz konkursów i olimpiad, ale są również niezbędne do pogłębiania wiedzy. My pokazaliśmy, że „matematyka jest melodią myśli”, a do przekazania tej melodii możemy wykorzystać narzędzie, które na co dzień służy nam do rozrywki. Taki również cel niesie za sobą portal Zadane.pl.
Organizatorzy olimpiady chcą, aby każdy uczestnik zapamiętał słowa Georga Polya: „Jeżeli chcecie nauczyć się pływać, to trzeba, żebyście weszli do wody. Jeżeli zamierzacie nauczyć się rozwiązywania zadań, to trzeba, żebyście je rozwiązywali”. |
|
|
 |
|

