|
|
 |
Niektórzy matematycy uważają, że wszystkie liczby są ciekawe. Jednak, niektóre z nich są bardziej interesujące niż pozostałe. Do tych wyjątkowo ciekawych liczb można na pewno zaliczyć liczbę π. Równie ciekawą liczbą, chociaż mniej znaną od π jest liczba, którą matematycy określają mianem „złotej liczby” i często oznaczają grecką literą ϕ.
Okazuje się, że liczbę ϕ można bardzo często spotkać przy okazji badania stosunków liczbowych występujących w przyrodzie. Już starożytni Grecy zauważyli, że wszystko to, gdzie występuje tak zwany „złoty podział”, jest piękniejsze niż to, gdzie złotego podziału nie ma. Zanim, więc przedstawię liczbę ϕ, wyjaśnię pojęcie „złotego podziału”.
Wyobraźmy sobie, że odcinek o długości a podzieliliśmy na dwa odcinki o długościach b i c (popatrz na rysunek złotego podziału odcinka a). |
|
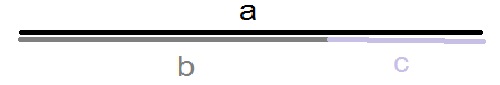 |
Jeżeli uda nam się dokonać podziału w taki sposób, że stosunek (iloraz) długości a całego odcinka do długości b dłuższego kawałka, będzie taki sam jak stosunek długości b dłuższego kawałka do długości c krótszego kawałka, czyli będzie zachodziła równość: |
|
to powiemy, że dokonaliśmy „złotego podziału” tego odcinka o długości a.
Ponieważ, jak widać na rysunku |
|
więc powyższe równanie można zapisać: |
|
co zachodzi wówczas, gdy: |
|
Tak więc liczba ϕ to po prostu wartość liczbowa stosunku długości dłuższego odcinka do długości krótszego odcinka otrzymana w trakcie „złotego podziału” odcinka.
Przekształcając powyższe równania można obliczyć wartość liczby ϕ. Jeżeli to zrobimy, dowiedziemy, że liczba ϕ jest liczbą niewymierną - nie da zapisać się jej w postaci ułamka zwykłego, w którym licznik i mianownik są liczbami całkowitymi i mianownik, oczywiście, jest różny od zera. Dokładnie liczba ϕ ma wartość: |
|
Można więc przyjąć w przybliżeniu, że: |
|
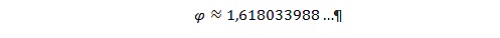 |
Liczba ϕ jest wszechobecna. Występuje ona w sztuce, architekturze, muzyce, a także w przyrodzie. Podam niektóre przykłady:
1. W idealnie zbudowanym ludzkim ciele można dopatrzeć się złotego podziału w bardzo wielu miejscach:
- linia pasa dzieli wzrost człowieka w „ złotym podziale”
- kolano dzieli nogę w „złotym podziale”
- stosunek długości głowy do jej szerokości jest równy liczbie ϕ
2. „Złotego podziału” można dopatrzeć się w budowie łodygi drzew, gdzie środkowy liść dzieli fragment łodygi między liśćmi w „złotym podziale”.
3. W proporcjach wielu budowli, można dostrzec liczbę ϕ. Wiele antycznych budowli powstawało na planie tak zwanego „złotego prostokąta” – prostokąta, w którym stosunek długości do szerokości jest równy liczbie ϕ.
Jedną z ciekawszych własności „złotego prostokąta” jest fakt, że po odcięciu od niego możliwie największego kwadratu, pozostały prostokąt jest nadal złotym prostokątem, który znowu można podzielić na kwadrat i „złoty prostokąt” itd. - aż w nieskończoność.
Prócz tego, że liczba ϕ jest gwarantem piękna, ma też ciekawe własności matematyczne. Oto niektóre z nich. Ponieważ: |
|
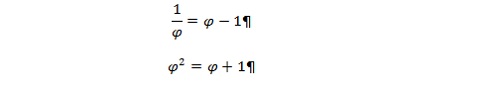 |
Jeśli piszemy już o liczbie ϕ nietrudno wspomnieć o ciągu Fibonacciego - właściwie Leonardzie z Pizy, który był włoskim matematykiem, żyjącym na przełomie XII i XIII w. Zajmował się głównie arytmetyką. Jednym z głównych jego osiągnięć jest rozpropagowanie w Europie hinduskiej notacji liczb, stosowanej do dzisiaj i nazywanej cyframi arabskimi.
W swoim dziele „Liber abaci” napisanym w 1202 r. Fibonacci podał wymyślony przez siebie problem o rozmnażaniu się królików. W rozwiązaniu tego problemu, autor podaje ciąg liczb (wielkości rodziny królików) rozpoczynający się od jedynek: 1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 510; 887; 1397; …. Kolejne wyrazy tego ciągu można tworzyć, pamiętając o tym, że dwa pierwsze wyrazy to 1 i 1, a każdy następny jest sumą dwóch wyrazów, które go poprzedzają, czyli: |
|
Zgodnie z powyższą zasadą mamy: |
|
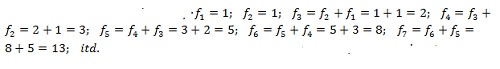 |
Właśnie ten ciąg nosi w matematyce nazwę ciągu Fibonacciego.
Podobnie jak liczba ϕ, liczby występujące w ciągu Fibonacciego często występują w przyrodzie. Oto kilka przykładów:
- w kształtach wielu roślin widać linie spiralne. Na przykład na owocu ananasa 8 takich linii biegnie w jedną stronę, a 5 lub 13 w przeciwną. Na tarczy słonecznika może się krzyżować 55 spiral z 89 (liczby te bywają większe). Również różyczki kalafiora ułożone są spiralnie.
- ilość płatków u wielu kwiatów jest równa liczbie, która występuje w ciągu Fibonacciego.
Jako ciekawostkę, warto nadmienić, że, jak odkryli, stosunkowo niedawno, naukowcy badający starożytne egipskie papirusy, ciąg, zwany przez nas ciągiem Fibonacciego i przypisywany temu właśnie matematykowi, znany był już i wykorzystywany praktycznie przez Egipcjan na kilka tysiącleci przed narodzinami Fibonacciego. Aby zrozumieć do czego Egipcjanie stosowali ciąg, zwany dzisiaj ciągiem Fibonacciego należy wspomnieć, że Egipcjanie w zapisie stosowali tylko ułamki proste, to znaczy takie, które w liczniku miały liczbę 1. Przykładami ułamków prostych są: |
|
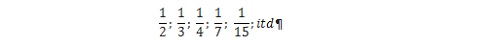 |
Jednak, na przykład, ułamek |
|
nie jest ułamkiem prostym, bo w liczniku występuje liczba 3. Takie ułamki Egipcjanie zapisywali jako sumę ułamków prostych i to co ciekawe, każdy składnik tej sumy miał inny mianownik np. |
|
Właśnie do rozkładu ułamka złożonego na sumę ułamków prostych, Egipcjanom potrzebny był omawiany przed chwilą ciąg Fibonacciego.
Spytacie się teraz, co wspólnego ma ciąg Fibonacciego, z liczbą ϕ? Aby odpowiedzieć na to pytanie, proponuję czytelnikom proste, ale bardzo pouczające ćwiczenie. Należy przygotować sobie zestaw kwadratów, których długości boków, są kolejnymi liczbami z ciągu Fibonacciego, a następnie budować z tych kwadratów coraz większy prostokąt, jak na poniższym rysunku. |
|
 |
Na początek z dwóch kwadratów o boku 1 tworzymy prostokąt 2 x 1. Dokładając do niego kwadrat o boku 2 otrzymujemy prostokąt 3 x 2. Następny prostokąt otrzymamy dodając do otrzymanego już prostokąta kwadrat o boku 3. Ten prostokąt będzie miał wymiary 5 x 3, i t d.
Prostokąt, przedstawiony na rysunku został zbudowany z 9 kwadratów o bokach: 1; 1; 2; 3; 5; 8; 13; 21 i 34, jednak nasi czytelnicy mogą pójść dalej, dokładając jeszcze dalsze, coraz to większe kwadraty. Następnie należy wyznaczyć długość i szerokość otrzymanego prostokąta i policzyć stosunek długości do szerokości. Prostokąt z rysunku jest prostokątem 55 x 34, a stosunek długości do szerokości wynosi |
|
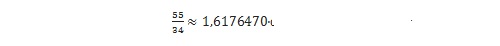 |
co jest bardzo bliskie liczby ϕ.
Ktoś, kto zbuduje jeszcze „większy” prostokąt (do jego budowy użyje większej liczby kwadratów) otrzyma w trakcie dzielenia jeszcze lepsze przybliżenie liczby ϕ. Oczywiście, otrzymany w ten sposób prostokąt, nie jest „złotym prostokątem” jednak może z powodzeniem go naśladować.”Podobieństwo” do „złotego prostokąta” będzie tym lepsze, im więcej kwadratów wykorzystamy do jego budowy. |
|
|
 |
|

