|
|
 |
CIEKAWE ZADANIA DO SAMODZIELNEGO ROZWIĄZANIA
|
|
Pojemność butli Butla wypełniona kwasem siarkowym ma masę M=19,34 kg. Ta sama butla tak samo wypełniona naftą ma masę m=9,1 kg. Jaka jest pojemność butli i jaka jest jej masa, gdy butla jest pusta, jeżeli gęstość kwasu siarkowego D=1834 kg/m3, a gęstość nafty d=810 kg/m3?
Zamiana trójkąta na prostokąt
Dowolny trójkąt ABC rozetnij dwoma cięciami na trzy części, tak by z tych części można było złożyć prostokąt.
Kwadrat i sześciokąty
Podziel kwadrat na 4 przystające sześciokąty.
|
|
Tajemniczy pierwiastek Pod literami A; B; C; D; E; F; G; H; I ukrywają się cyfry 1; 2; 3; 4; 5; 6; 7; 8; 9. Wskaż jaka cyfra ukrywa się pod każdą z liter jeśli prawdziwa jest równość: |
|
Gruba książka Do ponumerowania wszystkich stron pewnej księgi użyto 3389 cyfr. Ile stron liczy ta księga?
Polowanie na ryby
W zatoce jeziora są wbite 2 pale. Jeden pal wystaje nad wodę na wysokość 2 m, drugi na wysokość 1 m. Odległość między palami wynosi 10 m. Na każdym palu siedzi ptak czatujący na rybę. Prędkość lotu ptaka siedzącego na wyższym palu jest dwukrotnie większa od prędkości lotu ptaka siedzącego na niższym palu. Gdy na linii łączącej pale plusnęła ryba, ptaki zobaczyły ją jednocześnie i jednocześnie rzuciły się po zdobycz. W którym miejscu plusnęła ryba, jeżeli obydwa ptaki dopadły ją jednocześnie. |
|
Na czas
Internat pewnej szkoły znajduje się w znacznej odległości od niej i uczniowie muszą być wożeni do szkoły na godzinę 8 rano. Jeżeli autobus wiozący uczniów będzie jechał z prędkością 30 km/h, to zajedzie przed szkołę o 30 minut za wcześnie, jeżeli natomiast będzie jechał z prędkością 20 km/h, zajedzie o 30 minut za późno. Jaka jest odległość internatu od szkoły i z jaką prędkością powinien jechać autobus, aby zajechał przed szkołę punktualnie o godzinie 8 rano? W sklepie zoologicznym
Właściciel sklepu zakupił pewną liczbę sztuk zajęcy i pewną liczbę par królików. Liczba par królików była równa połowie liczby zajęcy. Za każdego zająca właściciel sklepu płacił po dwa dolary, a za każdego królika po 1 dolarze. Cena detaliczna, którą brał, była o 10 % wyższa za każde zwierzę (2,2 dolara i 1,1 dolara). Gdy wszystkie zwierzęta z wyjątkiem 7 były sprzedane, właściciel sklepu stwierdził, że wyłożona na ich kupno kwota zwróciła się. Jego czysty zysk stanowi więc wartość sprzedaną owych siedmiu pozostałych zwierząt. Jaki jest czysty zysk właściciela sklepu?
|
|
Tajemniczy iloczyn
Odtwórz następujący iloczyn. |
 |
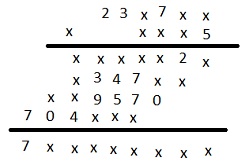 |
|
CZTERY EGIPSKIE UŁAMKI
a; b; c; d to liczby naturalne. Znaleźć rozwiązanie następującego równania:
Ile istnieje takich rozwiązań?
|
 |
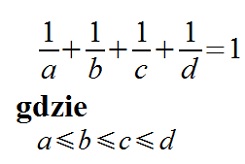 |
|
PODRÓŻE WAKACYJNE Przez pewną stację przejechały trzy pociągi specjalne, wiozące młodzież szkolną na kolonie. W pierwszym pociągu na kolonie jechało 462 dzieci; w drugim 546 dzieci, a w trzecim 630 dzieci. Oblicz z ilu wagonów składał się każdy pociąg, jeżeli wiadomo, że w każdym wagonie jechało tyle samo młodzieży i była to największa z możliwych liczba jadących w jednym wagonie.
PODZIAŁ PIENIĘDZY
Dwaj farmerzy: Adam i Bartek sprzedali stado owiec biorąc za każdą owcę tyle talarów, ile było w stadzie owiec. Zarobionymi pieniędzmi postanowili podzielić się po połowie. Najpierw podzielili między siebie banknoty. Po podziale banknotów okazało się, że Adam dostał o 10 talarów więcej niż Bartek. Pozostałe w bilonie pieniądze zabrał więc Bartek. Jednak, było tej reszty mniej niż 10 talarów. Aby powetować Bartkowi straty, Adam pozwolił mu jeszcze zabrać sakiewkę. Oblicz, jaka była wartość sakiewki.
GŁĘBOKOŚĆ DOŁU
Na pytanie przechodnia o docelową głębokość dołu kopanego właśnie przez robotnika, kopacz udzielił następującej odpowiedzi: „mój wzrost wynosi 1m i 80 cm. Gdy wykopię dół do końca, moja głowa będzie o tyle poniżej powierzchni ziemi, o ile teraz gdy już wykopałem połowę głębokości dołu, jest powyżej niej”. Jaka będzie głębokość dołu? |
|
ILE MIAŁEM PIENIĘDZY Wychodząc z domu miałem w kieszeni pewną liczbę złotówek i pięciozłotówek. Razem było więcej niż 140 zł, ale mniej niż150 zł. Wydałem trzecią część posiadanej gotówki. Po powrocie stwierdziłem, że pozostało mi tle złotówek ile przed wyjściem miałem pięciozłotówek i tyle pięciozłotówek ile początkowo miałem złotówek. Oblicz, ile pieniędzy miałem wychodząc z domu? Ile było tam złotówek, a ile pięciozłotówek?
TRUDNA ZAPŁATA
Kupujący ma zapłacić 37 zł. Problem jednak polega na tym, że kupujący ma w swoim portfelu same pięciozłotówki, a sprzedawca same dwuzłotówki. Pomóż im się rozliczyć.
TAJEMNICZA LICZBA
Na miejscu jednostek pewnej trzycyfrowej liczby stoi cyfra 2. Jeżeli tę cyfrę przeniesiemy na pierwsze miejsce, to otrzymamy liczbę, która od pierwotnej będzie o jedną trzecią większa. Jaka to liczba? |
|
ŻYCIORYS DIOFANTOSA
Młodość Diofantosa trwała 1/6 jego całego życia. Przez następne 1/12 swego życia Diofantos zapuszczał brodę. Dumny ze swej brody, przeżył następne 1/7 swego życia. Przez cały ten etap swojego dotychczasowego życia, Diofantos był kawalerem. 5 lat później, ożenił się i żona urodziła mu syna. Syn żył dokładnie połowę życia swego ojca. Diofantos zmarł 4 lata po śmierci syna. Ile lat żył Diofantos?
|
|
ZAKUP NASION ZBOŻA. Właścicielami pewnej farmy jest trzech braci: Adam, Bogdan i Karol. Pewnego roku uzgodnili oni, że zakupią nasiona pszenicy, by obsiać swoje pole. Adam i Bogdan pojechali dokonać zakupu, a Karol pozostał by na czas nieobecności braci doglądać farmy. Bogdan zakupił 75 worków pszenicy, a jego brat 45 worków. W domu postanowili, podzielić koszta zakupu pszenicy na trzy równe części. Ile dolarów musiał dać Karol Adamowi, a ile Bogdanowi jeżeli jego wkład w zakup zboża wynosił 1400 $? |
|
MISTRZOWIE LOGICZNEGO MYŚLENIA
Staszek i Piotr uważani są w szkole za najlepszych matematyków. Aby rozstrzygnąć, który jest z nich najlepszy, nauczyciel wymyślił dwie liczby, a następnie policzył sumę tych liczb i ich iloczyn. Sumę z policzonych liczb zapisał na kartce i podał Staszkowi, a iloczyn zapisany na drugiej kartce podał Piotrowi. Poinformował też obu chłopców, że pomyślane przez niego liczby są większe niż 2. Następnie zapytał się, czy któryś z uczniów na tej podstawie potrafi podać liczby pomyślane przez nauczyciela.
Staszek powiedział, że nie wie jakie to liczby.
Na to Piotr mu odpowiedział: Wiedziałem, że nie będziesz znał liczb, ale nie martw się, ja też ich nie znam.
Po tej wypowiedzi Piotra, Staszek stwierdził, że wie jakie to liczby.
Jakie liczby wymyślił nauczyciel?
|
|
TAJEMNICZE SUMY A; B; C to kolejne cyfry liczby trzycyfrowej ABC. Podobnie D; E; F to kolejne cyfry liczby trzycyfrowej DEF, a G; H; I to kolejne cyfry liczby trzycyfrowej GHI. Jakie cyfry ukrywają się pod literami A; B; C; D; E; F; G; H i I jeśli prawdziwa jest następująca suma: ABC+ DEF = GHI, ponadto każda cyfra jest inna i nie występuje cyfra zero Rozpatrz dwa przypadki.
a) liczba GHI jest możliwie najmniejsza
b) liczba GHI jest możliwie największa.
Podobnie przeanalizuj sumę ABC +DEF = GHIJ, uwzględniając, że jedna z cyfr jest zerem, lecz zerem nie jest ani cyfra A ani cyfra D ani cyfra G.
Dla uproszczenia przyjmij, że ABC |
|
SILOS ZBOŻOWY
Trzy silosy zbożowe mają następującą pojemność:
A – 8000 kg;
B - 5000 kg;
C – 3000 kg
A jest pełny, B oraz C są puste.
Czy potrafisz bez ważenia, przesypać 4000 kg do silosu A oraz 4000 kg do silosu B? |
|
GRA W TRZY KOPERTY
Jesteś uczestnikiem pewnej gry. Wejście do gry kosztuje 10 złotych. Gra polega na tym, że losujesz jedną kopertę spośród trzech. W jednej kopercie jest nagroda - 100 zł. Pozostałe dwie koperty są puste. Prowadzący pozwoli ci wybrać jedną kopertę, a następnie otworzy jedną z pozostałych kopert aby pokazać, że jest ona pusta. Następnie, prowadzący da ci wybór: pozostajesz przy swojej kopercie wybranej na początku, czy wybierasz pozostałą nieotwartą kopertę. Ponad to, oświadcza ci, jeszcze przed podjęciem przez ciebie decyzji, że jeżeli nie trafisz na pełną kopertę, to pozwoli ci jeszcze raz zagrać w tą samą grę bez dodatkowych opłat, jednak zwiększa tym razem zawartość wygrywającej koperty do 200 zł. Musisz, więc zadecydować: czy może lepiej przegrać pierwszą grę? Czy powinieneś zamienić kopertę? Następnego dnia, prowadzący informuje cię, jeszcze przed podjęciem przez ciebie gry, że jeżeli nie odnajdziesz pieniędzy w pierwszej rozgrywce, to pozwoli ci jeszcze raz zagrać, tym razem pula do wygrania będzie wynosiła 200 zł. Jeśli i tym razem też nie odnajdziesz pieniędzy, to możesz zagrać jeszcze trzeci ostatni raz. Tym razem o 300 zł. Gdy prowadzący poprosi cię o podjecie pierwszego wyboru - czy powinieneś zamienić kopertę, czy pozostać przy swoim początkowym wyborze?
Jakie decyzje będą dla ciebie najbardziej korzystne?
|
|
EGZAMIN TRZECH UCZNIÓW Trzej uczniowie muszą zdać egzamin z n przedmiotów. Ilość punktów jest przyznawana zgodnie z miejscem w rankingu wyników egzaminu. Osoba, która najlepiej zda dany egzamin, czyli znajdzie się na pierwszym miejscu, otrzyma największą ilość punktów za ten egzamin, następny jest uczeń na drugim miejscu, a uczeń na ostatnim trzecim miejscu otrzymuje najmniejszą ilość punktów za dany egzamin.
Za I miejsce na egzaminie przyznawane jest x punktów, za II miejsce na tym egzaminie – y punktów, a za III miejsce - z punktów. Uczeń B otrzymał x punktów z j. polskiego. Uczeń A otrzymał w sumie 22 punktów. Uczniowie B oraz C otrzymali każdy w sumie po 9 punktów.
Z ilu przedmiotów zdawali uczniowie egzamin, oraz jakie są wartości x; y i z? |
|
MLEKO
Mamy beczkę mleka a potrzebujemy odmierzyć tylko 1 litr mleka.
Jak to wykonać, jeżeli mamy do dyspozycji naczynie o pojemności 3 litry oraz naczynie o pojemności 5-litrów?
|
|
DZIEŃ SPOTKANIA Ponieważ moi przyjaciele z lat szkolnych mieszkają teraz w różnych miastach w całej Polsce, możemy się razem spotykać tylko raz do roku. Postanowiliśmy, że naszym miesiącem spotkań będzie zawsze sierpień. Natomiast dzień spotkania będzie co roku inny. Aby pamiętać o spotkaniu zaznaczaliśmy sobie dzień spotkania w kalendarzu. W tym roku nieszczęśliwie zgubiłem swój kalendarz z zaznaczoną datą spotkania. Postanowiłem więc zapytać o to moich kolegów. Niestety żaden z nich w czasie rozmowy telefonicznej ze mną nie miał pod ręką kalendarza z zaznaczoną datą i dlatego ich informacje były następujące:
Arek powiedział, że dzień spotkania jest liczbą parzystą
Basia stwierdziła, że liczba dnia jest większa od 13.
Czesio powiedział, że liczba dnia nie jest kwadratem żadnej innej liczby
Daria przysięgała, że liczba jest sześcianem pewnej innej liczby.
I na końcu Edward poinformował mnie, że data jest mniejsza od jednej czwartej jego wieku, który wynosi 68 lat.
Wczoraj dowiedziałem się, że tylko jedna z powyższych osób mówiła prawdę.
W jakim dniu odbędzie się spotkanie?
UCIECZKA PTAKÓW
W sklepie przyrodniczym, ktoś otworzył klatkę z ptakami i ponad 100 ptaków uciekło. Na początku w klatce było 300 ptaków. Miejscowa gazeta poinformowała, że z ptaków, które pozostały w klatce - 1/3 to zięby, 1/4 to papużki, 1/5 to kanarki, 1/7 to gwarki, oraz 1/9 to papugi. Początkowa ilość kanarków była trzy razy większa od ilości papug, które pozostały w klatce. Reporter artykułu pomylił się w jednym ułamku. Ile kanarków uciekło z klatki? |
|
|
 |
|

