|
|
 |
Małgorzata Jaszczuk-Surma
Zarys historii matematyki BABILOŃSKIEJ
Babilończycy zamieszkiwali rejon Mezopotamii, położony między Tygrysem a Eufratem. Stolicą Babilonii był Babilon. Pojawili się tam ok. 2000 r. p.n.e., po podbiciu Sumerów.
|
|
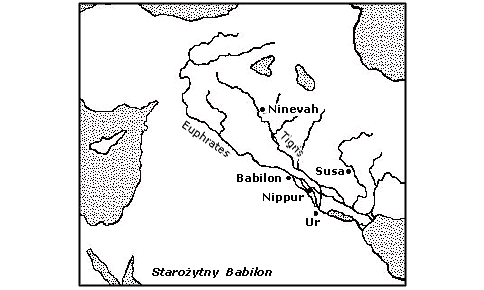 |
Mapa regionu, gdzie rozkwitała Babilońska cywilizacja
Sumerowie, którzy mieszkali na tych terenach przed 3500 r. p.n.e., stworzyli wspaniałą cywilizację. Budowali miasta, systemy nawadniania, mieli system prawny, administrację, a nawet pocztę. Posługiwali się sześć - dziesiętnym systemem liczbowym, jednak nie był to system pozycyjny.
Babilończycy natomiast posługiwali się pozycyjnym sześć - dziesiętnym systemem liczbowym. Podzielili dobę na 24 godziny, godzinę na 60 minut, a minutę na 60 sekund. Ta forma liczenia czasu przetrwała 4000 lat, aż do dziś. Chcąc napisać 5 godzin, 25 minut i 30 sekund, można to zrobić w postaci ułamków sześć - dziesiętnych: 5 25/60 30/3600.
W dziesiętnym ułamkowym systemie liczbowym wygląda to następująco:
5 4/10 2/100 5/1000, a w zwykłym systemie dziesiętnym: 5.425.
Babilończycy przejęli zdobycze naukowe i cywilizacyjne zarówno od Sumerów, jak i od Akkadian. Wielkim jednak ich osiągnięciem, poza pismem klinowym, była modyfikacja przejętego systemu liczbowego, w wyniku której powstał system pozycyjny. Niektórzy twierdzą, że było to ich największe osiągnięcie w matematyce. Niezwykłe jest to, że Babilończycy potrzebowali tylko dwóch różnych symboli do posługiwania się swoim sześć - dziesiętnym systemem liczbowym. W naszym dziesiętnym systemie mamy 9 symboli plus zero.
Pomimo że system liczbowy Babilończyków był systemem sześć - dziesiętnym pozycyjnym, to jednak wewnątrz niego istniały ślady systemu dziesiętnego. A to dlatego, że 59 liczb systemu sześć - dziesiętnego zbudowanych było z dwóch tylko symboli: jedności i dziesiątki.
|
|
 |
Oto 59 liczb zbudowanych z dwóch symboli
W pozycyjnym systemie liczbowym potrzebna jest reguła mówiąca o tym, które miejsce reprezentuje jakie jednostki. Na przykład liczbę 12345 można przedstawić następująco:
1 • 104 + 2 • 103 + 3 • 102 + 4 • 10 + 5
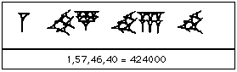
Czytamy tę liczbę od lewej do prawej strony. System Babilończyków zbudowany jest w podobnej konwencji - pozycja położona najbardziej na prawo przeznaczona jest dla liczb od 1 do 59. Jeśli przyjmiemy teraz symbole systemu sześć - dziesiątkowego, w którym liczby oddzielone są przecinkami, np.: 1,57,46,40, to liczba będzie wyglądać następująco:
1 • 603 + 57 • 602 + 46 • 60 + 40
Natomiast w systemie dziesiętnym ta liczba to: 424000.
|
|
Tak wygląda liczba 1,57,46,40 w babilońskim systemie liczbowym
|
 |
 |
|
W systemie babilońskim tkwią pewne pułapki. Liczbę 2 zapisuje się za pomocą dwóch symboli jedności, a 61 ma symbol 1 na pierwszym miejscu oraz drugi taki sam symbol na drugim miejscu, dlatego babilońskie liczby sześć - dziesiętne 1,1 oraz 2 są przedstawiane tak samo. Aby je od siebie odróżnić, umieszczano w zapisie dodatkowy odstęp. Tak więc w liczbie 2 oba symbole jedności stykają się wzajemnie i stają się pojedynczym znakiem graficznym, a w liczbie 1,1 między nimi stosuje się spację.
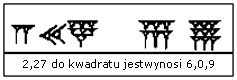
Pokażemy przykład działań matematycznych wyryty pismem klinowym na glinianej tabliczce (obecnie znajduje się w Muzeum w Luwrze, nr AO 17264), gdzie liczba 147 jest podniesiona do kwadratu:
w systemie sześć - dziesiętnym 147 = 2,27, a po podniesieniu do kwadratu otrzymujemy 1472 = 21609 [6,0,9].
|
|
Liczba 2,27 podniesiona do kwadratu |
 |
 |
|
W tym przypadku skryba pozostawił wolny odstęp między 6 i 9, który reprezentował zero, natomiast w liczbie 6,9 nie byłoby odstępu.
Najbardziej zadziwiającym aspektem zdolności matematycznych Babilończyków były wymyślone przez nich tabele obliczeniowe. W 1854 r. dwie takie tabele, datowane na ok. 2000 r. p.n.e., znaleziono w Senkerah nad Eufratem. Podane na nich są kwadraty liczb od 1 do 59 oraz sześciany liczb od 1 do 32. Na przykład tabliczka zawiera zapis: 82 = 1, 4, co oznacza:
82 = 1, 4 = 1 • 60 + 4 = 64 i tak dalej, aż do 592 = 58, 1 (58 • 60 + 1) = 3481).
Aby ułatwić sobie mnożenie, posługiwano się następującym wzorem:
ab = [(a + b)2 - a2 - b2]/2
Mnożyć można było według jeszcze innego algorytmu:
ab = [(a + b)2 - (a - b)2]/4
Jak więc widać, tabela z kwadratami liczb zawierała wszystko, co było potrzebne do mnożenia. Aby pomnożyć liczby przez siebie, wystarczyło wziąć z tabeli różnicę ich kwadratów, a następnie obliczyć 1/4 tej różnicy.
Z dzieleniem nie było jednak tak prosto. Było trudniejsze, gdyż Babilończycy nie wymyślili dla niego algorytmu. Działanie oparto na zasadzie, że
a/b = a • (1/b)
|
|
Jednym słowem, aby je wykonać, niezbędne było posiadanie tabel z ułamkami odpowiednich liczb. Takie tabele, z ułamkami liczb aż do kilku milionów, zachowały się do dzisiaj. Dzięki temu, posługując się symboliką sześć - dziesiętnego systemu liczbowego, możemy napisać, że porządek jednej z takich tabel obliczeniowych widzimy obok
W tabeli brakuje zapisu dla
1/7, 1/11, 1/13, itd.,
gdyż w omawianym systemie nie są to ułamki skończone. Nie oznacza to jednak, że Babilończycy nie mogli obliczyć któregoś z tych ułamków, np.
1/13,
gdyż robili to w następujący sposób:
|
 |
 |
|
1/13 = 7/91 = 7 • (1/91) = (około) 7 • (1/90)
Wartość 1/90 odczytywali już ze swoich tabel. Jeżeli w systemie
sześć - dziesiętnym dzielenie np. przez 7 dawało liczbę nieskończoną, wtedy skryba podawał liczbę najbliższą 1/7, a obok odnotowywał, że jest to przybliżenie, gdyż 7 nie jest podzielna.
Tabele obliczeniowe służyły również do rozwiązywania różnego typu równań, na przykład: n3 + n2.
Rozważmy takie równanie:
ax3 + bx2 = c
Należy wyjaśnić, że w celu przybliżenia czytelnikom tej problematyki, użyliśmy współczesnych symboli algebraicznych, a nie takich, jakimi posługiwali się Babilończycy. Rozwiązując powyższe równanie Babilończycy mnożyli obie strony równania przez a2 oraz b3, aby otrzymać:
(ax/b)3 + (ax/b)2 = ca2/b3
następnie wstawiali y = ax/b i otrzymywali równanie:
y3 + y2 = ca2/b3
które można rozwiązać wykorzystując tabelę obliczeniową z wartościami n3 + n2 dla wielkości n spełniających n3 + n2 = ca2/b3. Gdy obliczono wartość y,
wtedy również wartość x znajdowano z równania: x = by/a. Jeszcze raz podkreślamy, że wszystkie te działania nie były wykonywane zgodnie ze współcześnie stosowanymi symbolami algebraicznymi.
|
|
Równania liniowe ax = b rozwiązywano również za pomocą tabel, zachowując kolejność wykonywania działań. W tabeli z wartościami 1/n znajdowano wartość 1/a,
a następnie liczbę z systemu sześć-dziesiętnego podaną w tabeli mnożono przez b. Przypatrzmy się, jak skryba babiloński zapisał przykładowe zadanie:
Mamy 2/3 z 2/3 pewnej ilości jęczmienia, do której dodano jeszcze 100
jednostek jęczmienia. Wynikiem tej sumy jest prawdziwa ilość jęczmienia. Jaka to jest ilość?
Rozwiązanie podane przez skrybę wygląda następująco: mnożymy 0; 40 razy 0; 40 aby otrzymać 0; 26, 40. Odejmujemy to od 1; 00 i otrzymujemy 0; 33, 20. Odczytujemy odwrotność 0; 33, 20 z tabeli ułamków i otrzymujemy1; 48. Mnożymy 1; 48 przez 1, 40 i mamy rozwiązanie: 3, 0 w zapisie sześć-dziesiętnym.
Trzeba przyznać, że nie jest łatwo zrozumieć zapis skryby, chyba że przełożymy go na współczesny język algebraiczny i rozwiążemy równanie:
2/3 • 2/3 x + 100 = x
którego rozwiązanie jest równoważne rozwiązaniu równania (1 - 4/9)x = 100.
To dlatego skryba obliczył 2/3 2/3, wynik odjął od 1 i otrzymał (1 - 4/9),
a następnie znalazł w tabeli 1/(1 - 4/9) i w ten sposób znalazł x.
Babilończycy do rozwiązywania równań kwadratowych nie stosowali standardowych wzorów, natomiast rozważali dwa typy tych równań, tj.:
x2 + bx = c oraz x2 - bx = c
gdzie b i c są liczbami dodatnimi, ale niekoniecznie całkowitymi. Wzory rozwiązania tych równań wyglądały następująco:
x = √[(b/2)2 + c] - (b/2) i x = √[(b/2)2 + c] + (b/2)
|
|
Babilończycy nie opracowali wzoru na rozwiązywanie równań sześciennych. Trzeba było poczekać na to jeszcze trzy tysiące lat.
Na koniec nasuwa się pytanie: dlaczego Babilończycy posługiwali się sześć - dziesiętnym systemem liczbowym? Są różne teorie na ten temat i trudno tu wszystkie omówić. Przekonująca wydaje się teoria Neugebauera, który uważa, że pierwotnym systemem liczbowym Babilończyków był system dziesiętny. Jednakże po podbiciu Sumerów uległ on modyfikacji, żeby można było posługiwać się sumeryjskim systemem miar i wag, który był podzielny przez 3. Wiemy przecież, że Sumerowie posługiwali się ułamkami 1/3 oraz 2/3.
Inna teoria zakłada, że system ten przejęty został od Sumerów, dla których trójkąt równoboczny był podstawową figurą stosowaną w budownictwie, a kąt w takim trójkącie wynosi 60 stopni. Są również teorie, które widzą związek sześć - dziesiętnego systemu liczbowego z obserwacjami astronomicznymi starożytnych. Autorzy tych teorii sugerują, że liczba 60 jest wynikiem mnożenia ilości miesięcy księżycowych w roku przez ilość wówczas znanych planet (Merkury, Wenus, Mars, Jowisz, Saturn).
Wszelkie prawa zastrzeżone.
Żadna część artykułu nie może być kopiowana, cytowana lub wykorzystywana bez zgody wydawcy. Podstawa prawna: Ustawa o prawie autorskim i prawach pokrewnych z dn. 04.02.1994 r. Dz. U. Nr 24, poz. 83 z dn. 23.02.1994 r.
|
|
|
 |
|

